MixMatch文章解读+算法流程+核心代码详解

MixMatch

本博客仅做算法流程疏导，具体细节请参见原文 ## 原文 查看原文点这里 ## Github代码 Github代码点这里 ## 解读 MixMatch抓住了半监督算法的两个重要观点：第一是熵最小化；第二是一致性正则化。结合这两个观点的算法就形成了MixMatch。

熵最小化

半监督算法的一个常见假设就是分类的决策边界不应该通过数据分布的高密度区域。这句话简单的理解可以想象一个聚类模型，其决策边界一定是在簇与簇之间的稀疏边界上，不可能穿过一个簇的中心（高密度区域）。而实现这一点的一种方法就是要求分类器对未标记数据输出低熵预测。MixMatch中使用一个“sharpening”函数来隐式实现熵最小化。所谓熵最小化、低熵预测，都是指使输出概率分布比较有“偏向性”，而不希望输出一个“平均的预测”。熵在信息论中是不确定度的度量，根据离散模型的熵最大定理，可知在均匀分布时熵取得最大值，换句话说，出现一个确定的分布，即某一类的概率是1，其余类的概率是0时，熵为0。也就是说想要得到熵最小，就得使分类器输出后的模型预测概率集中分配给某一类。后面再介绍“sharpening”函数如何实现这一点。

一致性正则化

一致性正则化也是一个常见的半监督假设。VAT、MeanTeacher等其实都或多或少使用了这种假设。其核心在于，我们希望一个样本和其加扰版本（通常图像中称为Augment）通过分类器后，得到相似的输出。其实也就是说分类边界不应该穿过数据分布的高密度区域。如下图，红色点是原始样本，蓝色和绿色为其扰动版本，红色同心圆的虚线圆是我们期望的容差范围，即在这个区间类的都应该认为和其中心数据点为同一类。通过扰动数据点的加入，将决策边界推到合适的位置，使分类器的鲁棒性更强。

Consistency Regularization

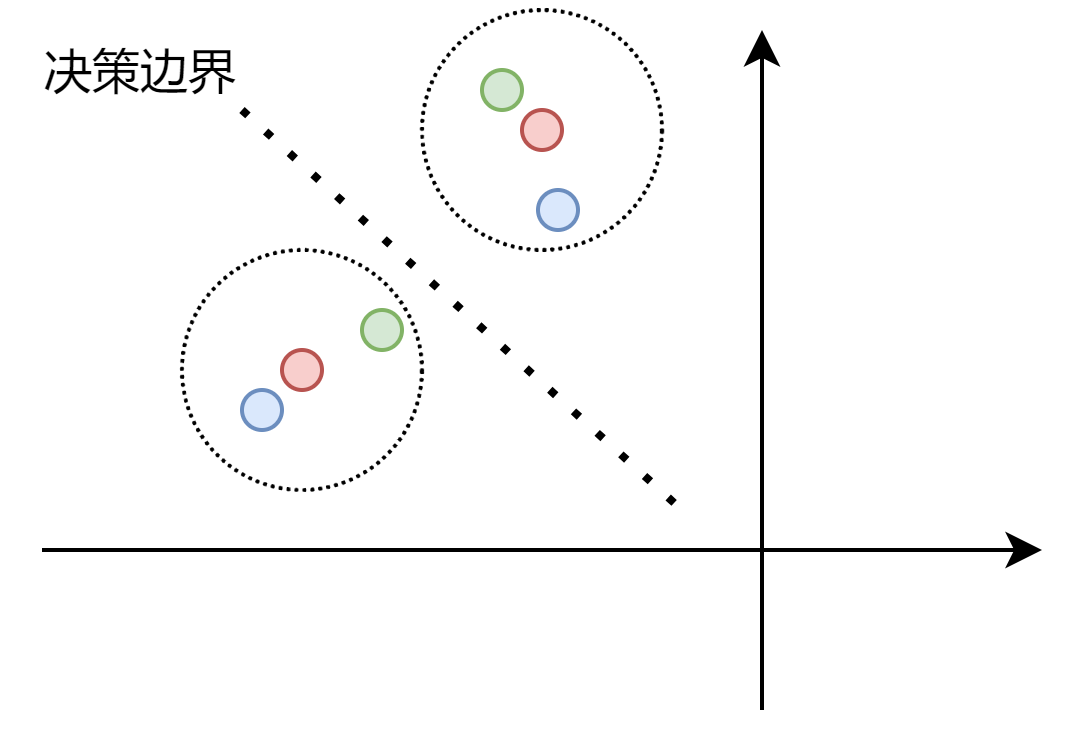
一般而言，通过对原始样本和其扰动版本的分类器输出进行衡量，即可实现一致性正则化，常见的衡量方式有MSE、KL散度、JS散度等。在MixMatch中通过对图像的标准数据增强(水平翻转、裁剪)实现扰动(Augment)，采用MSE准则方式衡量。

总得来说，算法有以下步骤：

屏幕截图 2021-07-31 154634

归结而言有五个步骤：

第一步，对数据进行扩增(Augment)。扩增分为对有标记数据集\(X\)的扩增和对无标记数据集\(U\)的扩增，分别记为\(\hat{X}\)和\(\hat{U}\)。对\(X\)扩增一次，对\(U\)扩增\(K\)次，文章中取\(K=2\)。因为在取batch时，\(Batch Size _U = BatchSize_X\)，所以扩增后\(Batch Size _{\hat{U}} = K\cdot BatchSize_{\hat{X}}\)。

第二步，计算平均预测分布。此步骤仅对数据集\(\hat{U}\)进行。即通过如下公式计算，其中\((\hat{u_{b,k}},y)\)是\(\hat{U}\)的一个\(Batch\)：

\(\bar{q_b}=\frac{1}{K}\sum_kP_{model}(y|\hat{u_{b,k}};\theta)\)

值得注意的是，\(P_{model}(y|\hat{u_{b,k}};\theta)\)是\(Softmax\)之后的预测概率分布。

第三步，通过\(sharpening\)函数完成分布的锐化，其计算公式如下：

\(Sharpen(p,T)_i=\frac{p_i^{\frac{1}{T}}}{\sum^L_{j=1}p_j^{\frac{1}{T}}}\)

当超参数\(T\to 0\)时，\(Sharpen(p,T)\)趋向于\(one-hot\)分布，即其中一个类别的概率为1，其余概率为0；锐化后的概率分布作为\(\hat{U}\)的数据标签(pseudo label)。

第四步，通过\(MixUp\)完成新数据集的构建。先将第一步扩增后的\(\hat{X}\)和\(\hat{U}\)进行拼接再打乱顺序，得到\(W=Shuffle(Concat(\hat{X},\hat{U}))\)，然后再将\(W\)分为两部分，第一部分大小与\(\hat{X}\)相同(也与\(X\)相同)，记为\(W_x\)；第二部分大小与\(\hat{U}\)相同(也与\(U\)相同)，记为\(W_u\)。然后将\(W_x\)和\(\hat{X}\)进行\(MixUp\)，\(W_u\)和\(\hat{U}\)进行\(MixUp\)，得到\(X'\)和\(U'\)。\(MixUp\)步骤如下： \(\lambda\sim Beta(\alpha,\alpha)\) \(\lambda'=max(\lambda,1-\lambda)\) \(x'=\lambda'x_1+(1-\lambda')x_2\) \(p'=\lambda'p_1+(1-\lambda')p_2\)

第五步，计算半监督损失函数，分为在标记数据集\(X'\)上的损失函数\(L_x\)和在无标记数据集\(U'\)上的损失函数\(L_u\)，公式如下：

\(L_x=\frac{1}{|X'|}\sum_{x,p\in X'}H(p,P_{model}(y|x;\theta))\)

\(L_u=\frac{1}{L|U'|}\sum_{u,q\in U'}||q-P_{model}(y|u;\theta)||^2_2\)

\(L=L_x+\lambda_UL_u\)

其中\(H(\cdot)\)是\(CorssEntropyLoss\)；\(L_u\)其实就是\(MSE\)准则下的误差项。

反向梯度传播即可完成整个MixMatch算法

核心代码详解

图像的水平翻转、裁剪实现\(Augment\)：

transform_train = transforms.Compose([
    dataset.RandomPadandCrop(32),
    dataset.RandomFlip(),
    dataset.ToTensor(),
])

transform_val = transforms.Compose([
    dataset.ToTensor(),
])

这里是在迭代过程中，手动取迭代器中的batch，而不是直接使用Dataloader。这种做法在最近的几篇文章代码复现中都遇见了，其主要目的是为了在一个epoch中可以迭代指定次数，而直接使用Dataloader只能迭代最多\(ceil(\frac{样本总数}{BatchSize})\)次，其中\(ceil(\cdot)\)是上取整函数，如果\(drop_last\)，则只能迭代\(\frac{样本总数}{BatchSize}\)次。代码中的两个try except是为了保证迭代器完全迭代一次后，重新加载迭代器，继续迭代，直到达到指定次数才跳转下一个epoch。

for batch_idx in range(args.train_iteration):
     try:
         inputs_x, targets_x = labeled_train_iter.next()
     except:
         labeled_train_iter = iter(labeled_trainloader)
         inputs_x, targets_x = labeled_train_iter.next()

     try:
         (inputs_u, inputs_u2), _ = unlabeled_train_iter.next()
     except:
         unlabeled_train_iter = iter(unlabeled_trainloader)
         (inputs_u, inputs_u2), _ = unlabeled_train_iter.next()

因为文章中取\(K=2\)，所以进行两次扩增，求输出概率的均值，其中output_u和output_u2分别为两次扩增后的模型输出结果：

outputs_u = model(inputs_u)
outputs_u2 = model(inputs_u2)
p = (torch.softmax(outputs_u, dim=1) + torch.softmax(outputs_u2, dim=1)) / 2  # 求两次的平均值

求Sharpening结果:

pt = p**(1/args.T)
targets_u = pt / pt.sum(dim=1, keepdim=True)
targets_u = targets_u.detach()

完成\(MixUp\):

all_inputs = torch.cat([inputs_x, inputs_u, inputs_u2], dim=0)
all_targets = torch.cat([targets_x, targets_u, targets_u], dim=0)
l = np.random.beta(args.alpha, args.alpha)
l = max(l, 1-l)
idx = torch.randperm(all_inputs.size(0))
input_a, input_b = all_inputs, all_inputs[idx]
target_a, target_b = all_targets, all_targets[idx]
mixed_input = l * input_a + (1 - l) * input_b
mixed_target = l * target_a + (1 - l) * target_b

然后计算损失函数:

logits = [model(mixed_input[0])]
for input in mixed_input[1:]:
    logits.append(model(input))
# put interleaved samples back
logits = interleave(logits, batch_size)
logits_x = logits[0]
logits_u = torch.cat(logits[1:], dim=0)

Lx, Lu, w = criterion(logits_x, mixed_target[:batch_size], logits_u, mixed_target[batch_size:], epoch+batch_idx/args.train_iteration)

loss = Lx + w * Lu

反向梯度传播，结束。