知识储备-卷积/滤波及Matlab实现

通信基础-卷积/滤波(原理及Matlab实现)

原理

若有两个在定义域上可积的函数\(f(x)\)和\(g(x)\)，波形如下：

55f37ca13c8e2d21fb00aa2bf65c6d1

则卷积的定义为：

连续形式：\(f(x)*g(x)=\int^{\infty}_{-\infty}g(\tau)f(x-\tau)\)

离散形式：\(f(n)*g(n)=\sum_{i=-\infty}^{\infty}g(i)f(n-i)\)

看起来略微有点复杂，其物理意义就是将可积函数\(f(x)\)前后翻转颠倒（卷积中的-卷）；再进行相乘求积分/求和（卷积中的-积）。

f61355f876f0b6176d5b3f2767a0395

对应的步骤拆解为上图，可以把\(g(x)\)看做一个窗，这个窗固定不动，\(f(x)\)在翻转后，从左到右进入窗，并与窗对应点相乘并求和/积分，当\(f(x)\)穿过整个窗后，卷积运算结束。

Matlab仿真

有两种实现方式，第一种是调用其filter函数；第二种是手动运算。 ### 滤波器设计 设计一个简单的低通滤波，分离开2KHz和4KHz。 ### filter函数

% 测试卷积
clc;clear;close all;
Fs = 20000; %采样率
fc1 = 2000; %第一个正弦波频率2Khz
fc2 = 4000;% 第二个正弦波频率4Khz
N = 4096;%fft点数
t = 0:1/Fs:100/Fs;%时间序列
y1 = cos(2*pi*fc1*t);% 第一个正弦波
y2 = cos(2*pi*fc2*t);% 第二个正弦波
figure(1)
subplot(211)
plot(t, y1, 'b')
xlabel('t')
title('f=2KHz正弦波')
subplot(212)
plot(t, y2, 'r')
xlabel('t')
title('f=4KHz正弦波')
figure(2)
subplot(211)
y_mix = y1+y2;% 混合信号
plot(t, y_mix)
title('2KHz和4KHz信号混合后的波形')
subplot(212)
x = 0:Fs/N:(N-1)/N*Fs; %频率序列
plot(x, abs(fft(y_mix, N)))% 做N点fft
xlabel('Hz')
title('混合后的频谱图')
%使用自带filter函数滤波
filter_coffe = load('filter_coffe');% 读取滤波器系数，可直接使用filter designer设计低通滤波器
filter_coffe = filter_coffe.Num;
filter_after = filter(filter_coffe, 1, y_mix);% 使用filter函数滤波
figure(3)
subplot(211)
plot(t, filter_after)
title('使用filter函数滤波后时域图')
xlabel('t')
subplot(212)
plot(x, abs(fft(filter_after, N)))
title('使用filter函数滤波后频域图')
xlabel('Hz')

手动实现

过程就和上面第一点中讲的完全相同，先翻转一个信号，再依点送入并和另外一个信号对应相乘求和/积分。

% 自己定义滤波 先倒过来，然后一步一步往里推数据，再相乘求和。数据窗长应该和滤波器系数长度相同
fft_data = zeros(length(filter_coffe), 1); %准备数据窗长
y_fft_in = zeros(length(filter_coffe)-1+length(y_mix), 1);% 先准备一个全0序列
y_fft_in(length(filter_coffe):end, 1) = y_mix(end:-1:1);% 给全0序列后面填翻转后的数据。整个过程等于在给原始数据前面补0
y_fft_out = zeros(length(y_mix), 1);% 准备输出数据的位置
for step=1:1:length(y_mix)   
    y_fft_out(step) = filter_coffe*y_fft_in(step:step+length(filter_coffe)-1); %相乘求和
end
figure(4)
subplot(211)
plot(t, y_fft_out)
title('手动实现滤波的时域图')
xlabel('t')
subplot(212)
plot(x, abs(fft(y_fft_out, N)))
title('手动实现滤波的频域图')
xlabel('Hz')

结果

先产生两个频率的正弦波，并混合。 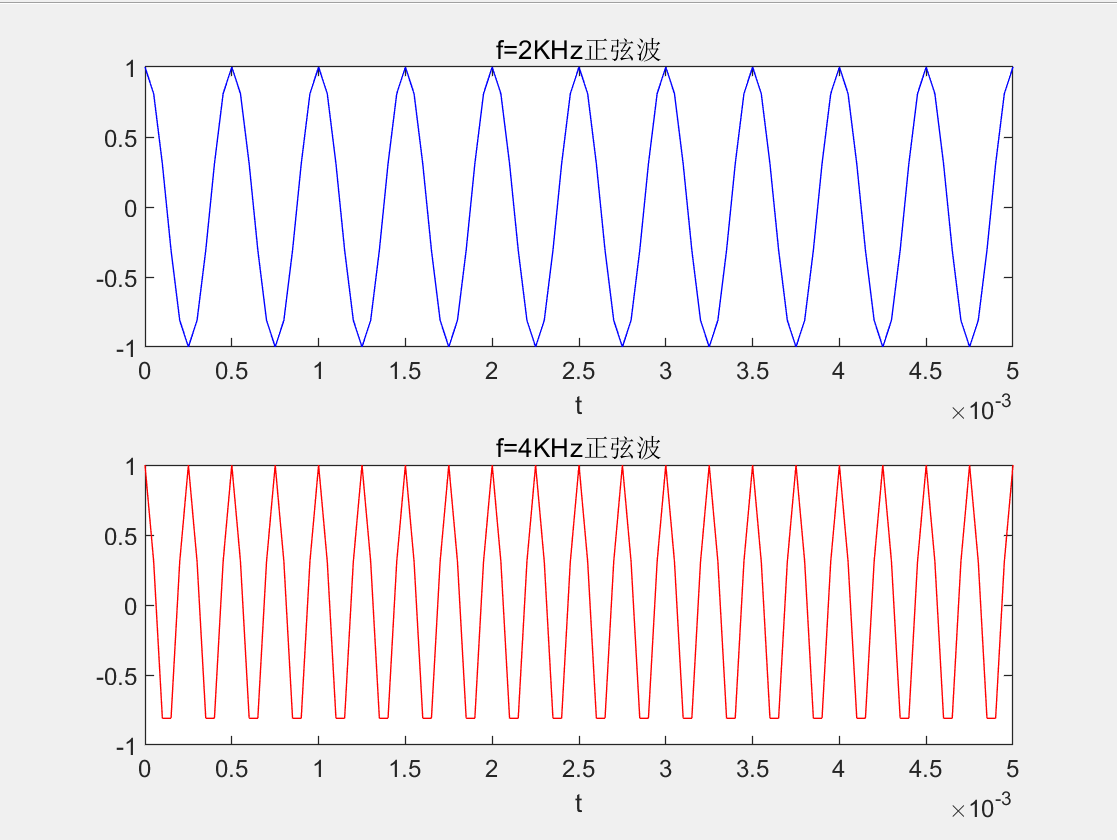混合后的时域和频域波形 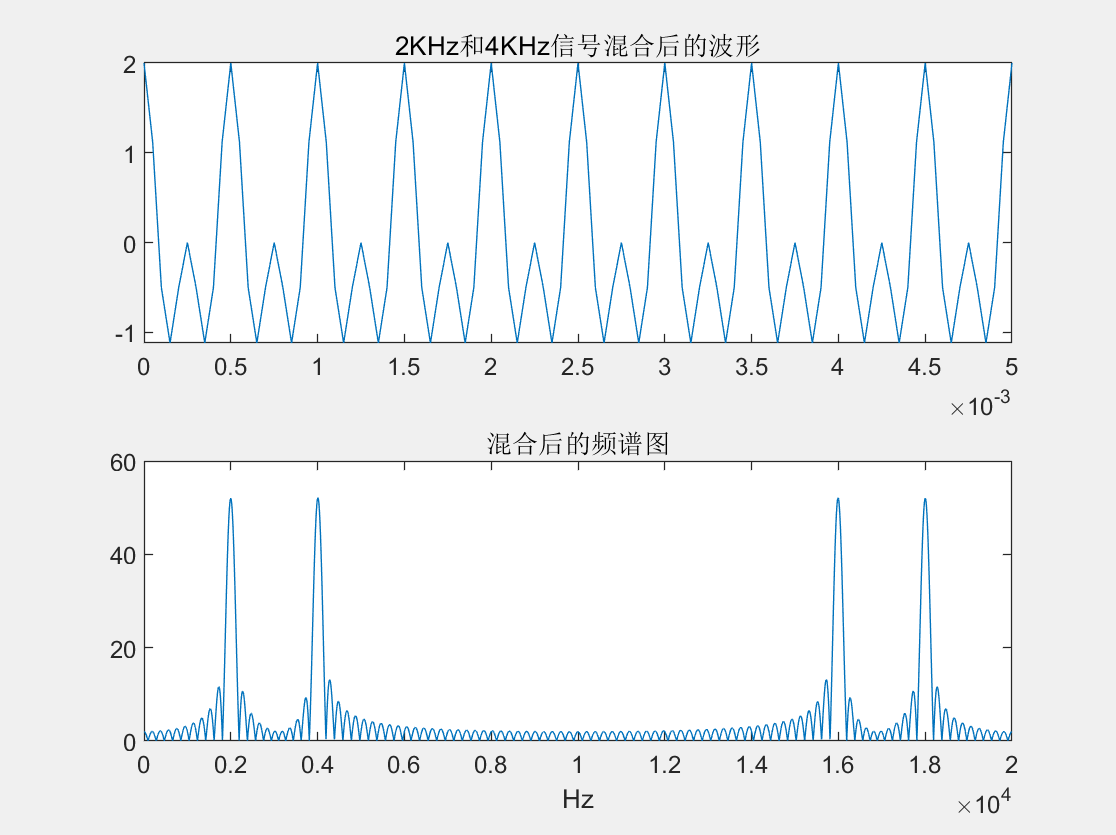使用filter函数滤波结果 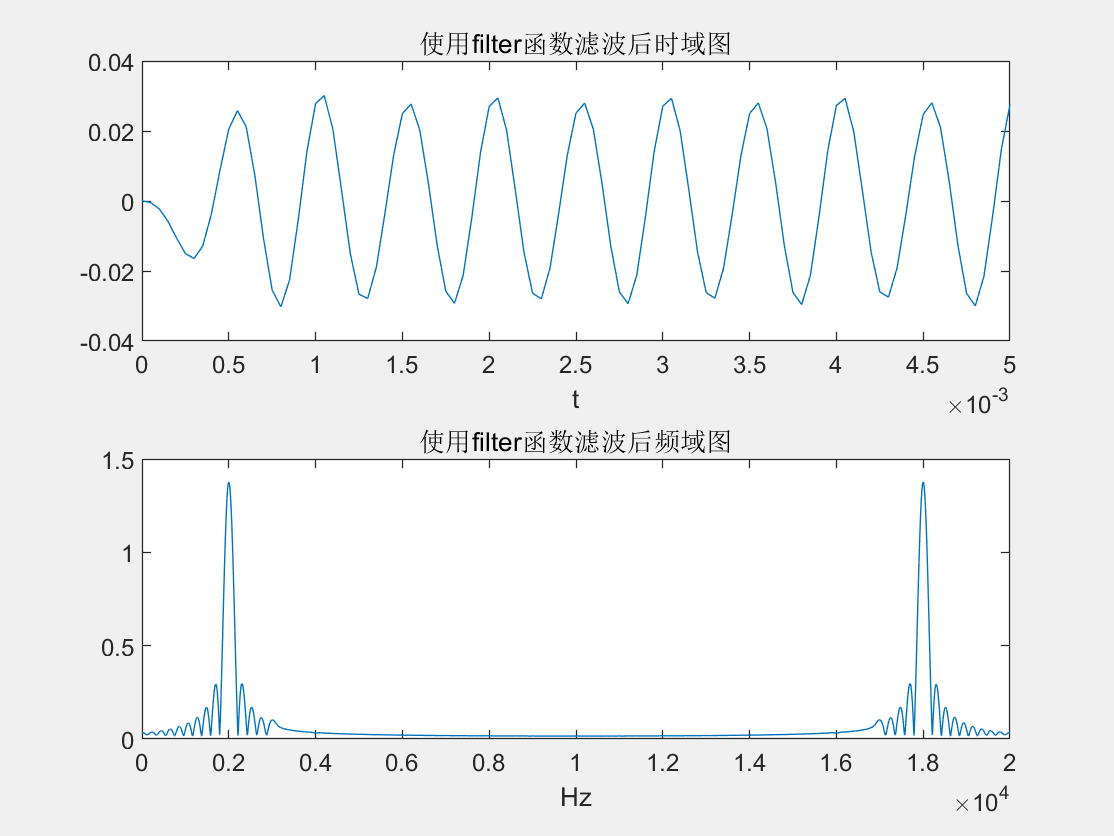使用自定义方法滤波: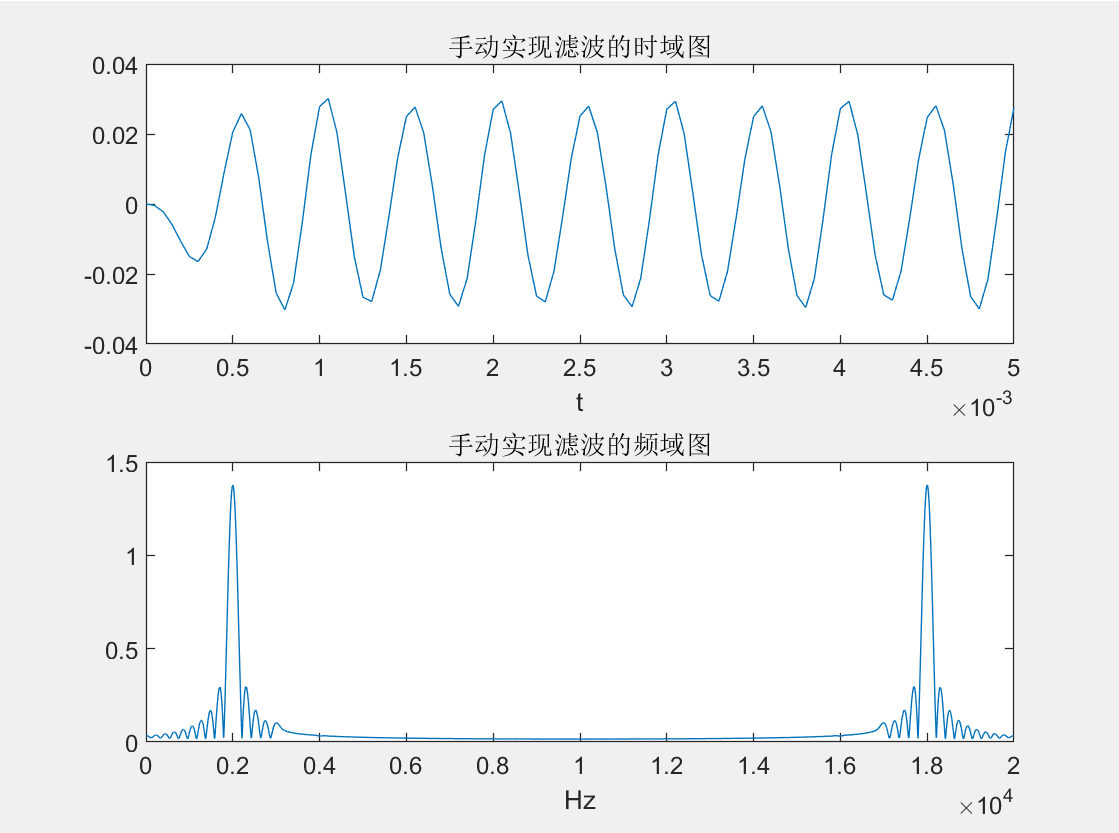

补充（与相关的关系）

• 卷积=补零->翻转->Hadamard积->求和
• 相关=补零->Hadamard积->求和

$$ \[\begin{aligned} &x=[3,6,2] \\ &y=[2,1,0]\\ \\ &r_{x y}(-2)=\quad \begin{array}{lllll} &&3 & 6 & 2\\ 2 & 1 & 0&&&=3\times 0=0 \end{array}\\ \\ &r_{x y}(-1)=\quad \begin{array}{lllll} &3 & 6 & 2\\ 2 & 1 & 0&&&=3\times 1+6\times0=3 \end{array}\\ \\ &r_{x y}(0)=\quad \begin{array}{lllll} 3 & 6 & 2\\ 2 & 1 & 0&&&=3\times 2+6\times1+2\times0=12 \end{array}\\ \\ &r_{x y}(1)=\quad \begin{array}{lllll} 3 & 6 & 2\\ &2 & 1 & 0&&&=3\times 0+6\times2+2\times1=14 \end{array}\\ \\ &r_{x y}(2)=\quad \begin{array}{lllll} 3 & 6 & 2\\ &&2 & 1 & 0&&&=2\times2=4 \end{array}\\ \end{aligned}\]

$$