知识储备-OFDM

OFDM

  • 宽带系统： 发送信号通过多条有显著时间的路径到达接收端， 产生干扰（也就是著名的多径干扰）。
  • 窄带系统： 发送信号通过一条或多条没有时间差的路径到达接收端， 没有干扰（相当于简单的叠加）。

可以简单认为，系统带宽为\(B=1/T_B\)，即系统带宽约等于码元周期的倒数；而发射的信号，由于多经，最大的延时时间为\(\tau_{max}\)，当\(\tau_{max}<T_B\)时，即在第二个码元发射时，第一个码元已经完全接收，所以不会产生多径干扰和码间干扰，认为是窄带系统

为了提高传输速率，\(1/T_B\)会增大，即会出现\(\tau_{max}>T_B\)。当前数据还没接收完毕，那么当前数据的最后一条径和下一个数据的第一条径就会重叠，产生多径干扰和码间干扰。数据的一部分会加强，一部分会减弱，在频域内表现为频率选择性衰落，认为是宽带系统

对于相同的场景， 相同的时延， 传输带宽不同， 决定了系统到底有没有多径干扰。

为了将宽带系统\(\to\)窄带系统，速率不公\(\to\)频分复用，所以推出OFDM调制

OFDM介绍[5]

是一种多载波的传输方法，将频带划分为多个子带（子信道）进行并行传输，将高速数据流分为多个并行的低速数据流，然后调制到每个信道的子载波上进行传输。

  • 各个子载波之间相互正交，以便接收端能够完全地分离各路信号。
  • 为了提高频谱利用率和增大传输速率，各路子载波的已调信号频谱有部分重叠。
  • 每路子载波的调制是多进制调制，而且每路子载波的调制制度可以不同。可以根据各个子载波处信道特性的优劣不同采用不同的体制。

主要优势：OFDM能很好地对抗频率选择性衰落和窄带干扰。在多载波系统中，每一时刻只会有少部分的子信道收到深衰落的影响。

##　数学模型

OFDM子带信号形式

假设在一个OFDM系统中有\(N\)个子信道，每个子信道采用信号为： \[ x_k(t)=B_kcos(2\pi f_kt+\varphi_k)\quad\quad k=0,1,\cdots,N-1 \] 式中：\(B_k\)为第\(k\)路子载波的振幅，它受基带码元的调制；\(f_k\)为第\(k\)路子载波的频率；\(\varphi_k\)为第\(k\)路子载波的初始相位，则在此系统中\(N\)路子信号之和可以表示为： \[ \begin{align} e(t)=\sum\limits_{k=1}^{N-1}x_k(t)=\sum\limits_{k=1}^{N-1}B_kcos(2\pi f_kt+\varphi_k) =\sum\limits_{k=1}^{N-1}\textbf{B}_ke^{j(2\pi f_kt+\varphi_k)} \end{align} \] 其中，\(\textbf{B}_k\)是一个复数，为第\(k\)路子信道中的复输入数据。

正交化

为了使这\(N\)路子信道信号在接收时能够完全分离，要求他们满足正交条件。在码元持续时间\(T_B\)内任意两个子载波都正交： \[ \int^{T_B}_0\cos(2\pi f_kt+\varphi_k)\cos(2\pi f_it+\varphi_i)=0 \] 具体推导见书本[1]。

结果是要求子载频满足 \[ f_k=k/2T_B \] 且要求子载频间隔： \[ \Delta f=f_k-f_i=n/T_B \] 即最小子载频间隔为： \[ \Delta f_{min}=1/T_B \] 多路子载波频谱的模

看起来各路子载波的频谱重叠，但是实际上在一个码元持续时间内它们是正交的。所以可以用此正交特性将各路子载波分离开。

采用不同的调制方式，仅幅度和相位有变化，不破坏其正交性。

其总带宽为： \[ B_{OFDM}=\frac{N+1}{T_B}(Hz) \] 为什么是\((N+1)\)而不是\(N\)？？

具体实现

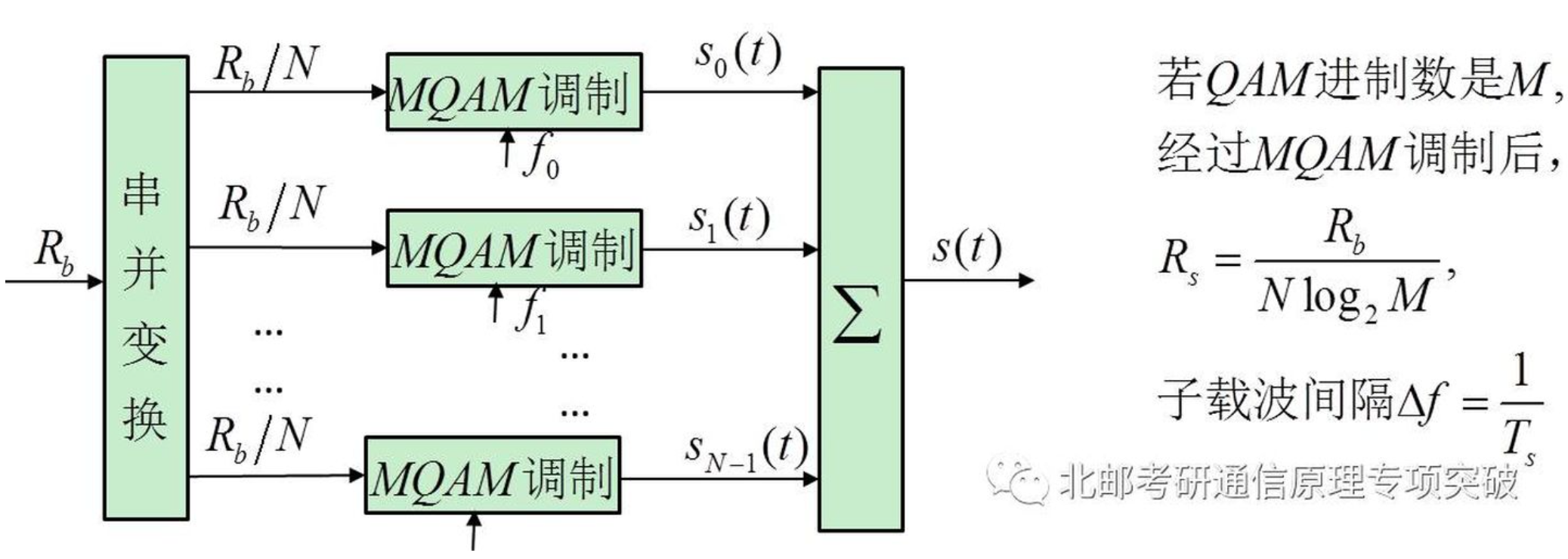
MQAM的OFDM实现

以MQAM为例。由于OFDM信号表示式的形式如同逆离散傅里叶变换式(IDFT)，所以可以用计算IDFT和DFT的方式进行OFDM的调制和解调[2]。还可以参考blog[6]

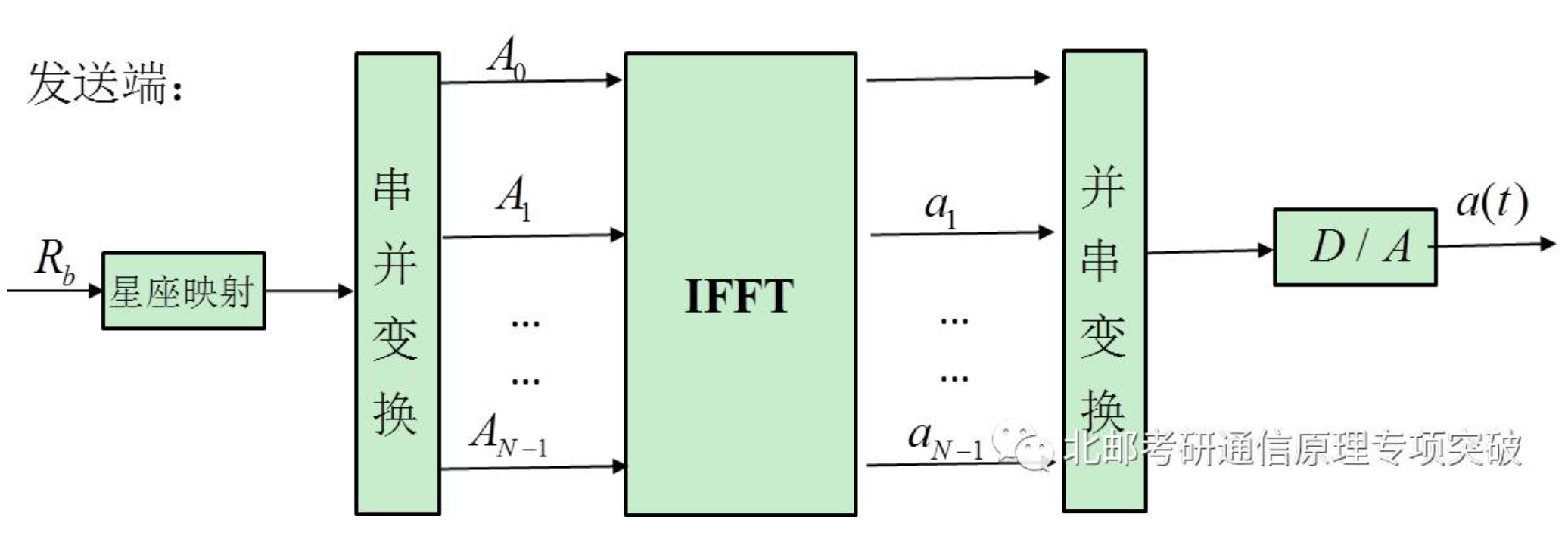
OFDM数字化处理框图-发射端

OFDM数字化处理框图-接收端

详细推导及实现结构可以参考资料[4]，简而言之就是\(N\)路用\(N\)个正交子载波进行调制，最后在时域相加，则有： \[ s(t)=\sum\limits_{n=0}^{N-1}s_ie^{j2\pi f_it} \] 这不和离散傅立叶变换差不多嘛。

拓展

由于多径效应，可能会产生干扰（信号经过不同的信道，所带来的延时不同）

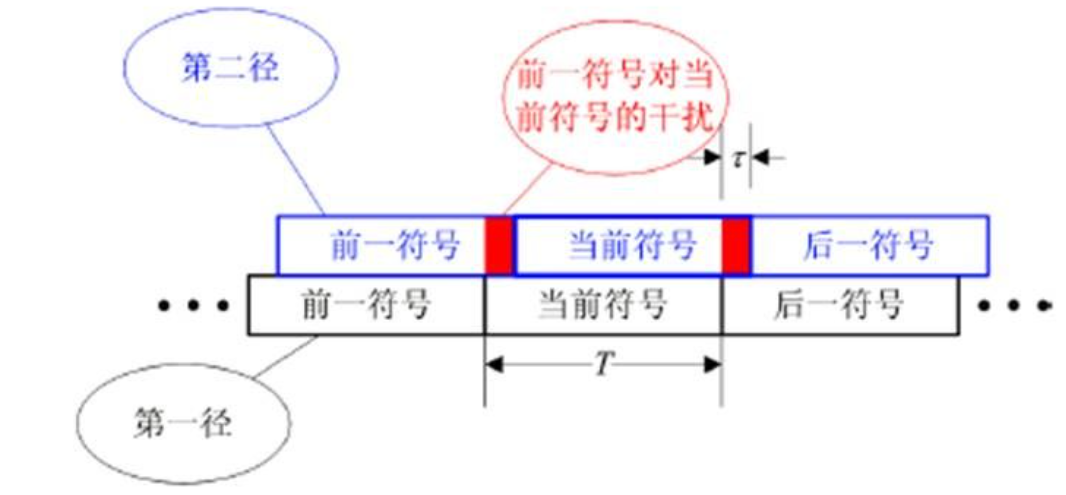
多径干扰的示意图

引入保护间隔：

  • 补零
  • 插入循环前缀（cp）或循环后缀（cs）

一般采用循环前缀，即将OFDM的后部的采样复制到前面，长度为\(T_{cp}\)，故每个符号的长度为\(T_{sym}=T_{B}+T_{cp}\)且\(T_{cp}\)大于等于多径时延。

符号之间的关系[3]

符号 意义
\(T_B\) 有效数据部分时间
\(T_{cp}\) 循环前缀长度
\(T_{sym}\) OFDM符号长度，\(T_s=T_B+T_{cp}\)
\(N\) 子载波数
\(\Delta f\) 子载波间隔，\(\Delta f=\frac{1}{T_B}\)
\(B\) 带宽，\(B=(N+1)\Delta f\)
\(T_{sample}\) 采样时间间隔，\(T_{sample}=\frac{1}{B}=\frac{T_B}{N+1}\)
\(F_s\) 采样频率，\(F_s=\frac{1}{T_{sample}}=\frac{N+1}{T_B}\)

OFDM的特性补充

  • 抗频率选择性衰落信道：由于串转并，将高码率的数据流转换为低码率的，使得每个子载波等价于窄带系统。从而对于每个子载波而言（调制和解调都可以认为是在子载波上的操作），频率选择性衰落影响不大（在窄带面前都可以认为是频率衰落平坦的），从而说明了OFDM的抗频率选择性衰落。

image-20240123163514071

  • Others todo…

20240118 update

Diagram of legacy OFDM PHY

image-20240118153805786

Exemplary OFDM coherence slot and time-domain waveform

image-20240118153824808

An OFDM symbol contains \(N=32\) subcarriers, and \(G=10\) DC guard band and edge guard band among the subcarriers.

A subcarrier in an OFDM symbol (the yellow column) is refereed to as a resource element (RE). And a coherence slot contains \(F=8\) OFDM symbols, with \(P=7\times 8=56\) pilot REs and \(D=16\times8=128\) data REs, respectively.

The length of a time-domain full OFDM symbol is \(S=N+N_{CP}\)​.

20250327 Update

OFDM的格式

OFDM调制完后，是按一个完整OFDM的纬度去并转串的。

OFDM的正交性

OFDM一直给我了一个误区，就是正交性似乎是成型滤波/FFT这些带来的。但是实际上，是由于发射基带信号是一个矩形波，在频域上是sinc函数，所以有周期性的零点。参考[https://blog.csdn.net/madongchunqiu/article/details/18614233]

img

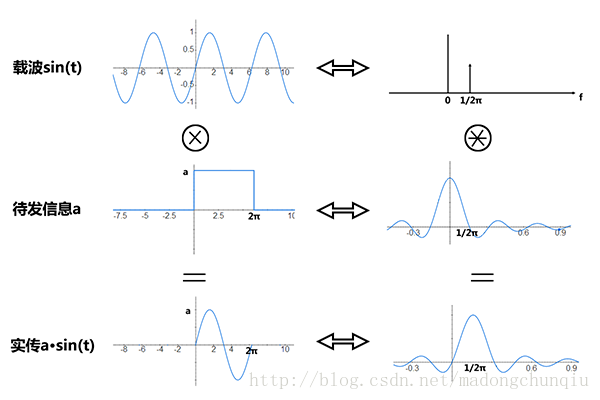
再来一个：

img

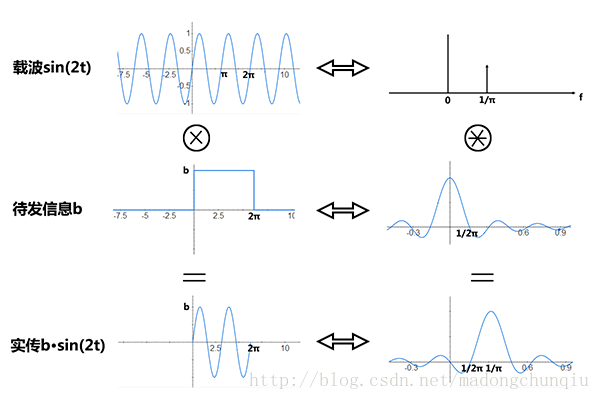
叠在一起后是：

img

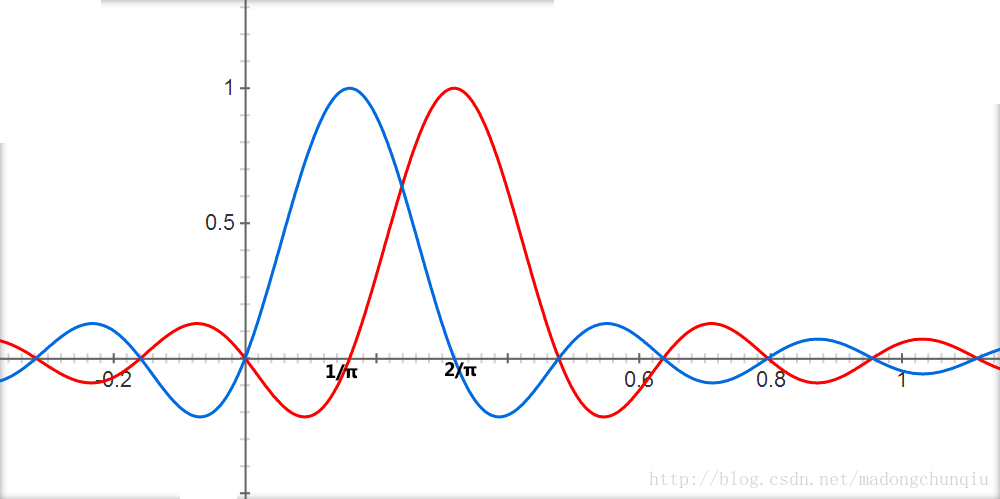
可以观察到本身就存在零点。然后，成型滤波可以加强这个零点（因为可能存在非完美矩形波形，导致子载波泄露，可以参考https://lcjoffrey.top/2025/03/27/recuPulseandtrapezoidPulse/）

然后，通过上采样，成型滤波，将带宽限。构成OFDM。

但是在实际工程中，还需要在时域加窗，可以参考https://blog.csdn.net/a2145565/article/details/139580022

OFDM-IM ( OFDM with Index Modulation)

OFDM-IM, OFDM with Index Modulation

OFDM-IM技术的核心思想是子载波在发送端被分成两部分，一部分子载波是激活的，称为有效子载波。==这部分载波来传输星座点==，而另一部分并不传输信号，==将载波的非激活和激活的状态信息作为额外信息进行传输==

OFDM-IM系统在整体的信号处理过程与OFDM系统基本一致。而两者的主要区别主要为：在OFDM系统中，所有的子载波都用来传输调制好的信号，所有比特信息都承载在载波所发送的信号上。但在加入了索引思想之后，OFDM-IM系统在发送端会先将所有的子载波分为若干个块，而所需传输的比特信息也相应的被分成了相同数量的分组，并且每个分组中比特又被划分为了两部分：索引比特和调制比特。其中，索引比特的部分是用来确定有效载波在子块中的位置信息，调制比特是用来生成调制符号并通过有效子载波进行发送。

image-20240418183904747

image-20240418183935551

当\(\eta\neq\mathbf{I}_\beta\)时，\(x_\beta(\eta)=0\)，等于是在该子载波上静默。

image-20240418184214775

image-20240418184226034

传输信息量由两部分组成。

Reference

  1. P243-P244 樊昌信, and 曹丽娜. 通信原理.第7版. 国防工业出版社, 2012. ↩︎
  2. P245-P245 樊昌信, and 曹丽娜. 通信原理.第7版. 国防工业出版社, 2012. ↩︎
  3. https://zhuanlan.zhihu.com/p/57967971 ↩︎
  4. https://zhuanlan.zhihu.com/p/30538458 ↩︎
  5. https://zhuyulab.blog.csdn.net/article/details/109907244 ↩︎
  6. https://zhuyulab.blog.csdn.net/article/details/111075990 ↩︎
basic knowledge
#OFDM
知识储备-OFDM
https://lcjoffrey.top/2022/03/01/introductionofOFDM/
作者
Joffrey
发布于
2022年3月1日
更新于
2025年3月27日
许可协议