Supervised Learning for Channel Estimation
Deep Channel Learning for Large Intelligent Surfaces Aided mm-Wave Massive MIMO Systems. Ahmet M. Elbir et.al. IEEE Wireless Communications Letters, Sept. 2020 (pdf) (Citations 51)
其余细节可以参考我的论文笔记
缩写说明
- LIS: Large Intelligent Surface==Intelligent Reflecting Surface
- NMSE: Normalized Mean-Square-Error
Quick Overview
提出一种基于监督学习的IRS信道估计,对一个用户K,信道分为direct channel 和 cascaded channel:
direct channel:只有1个信道
cascaded channel of IRS with L elements:有L个信道,即每个element都有一个级联信道,从BS->element->User K
每个用户有两个一样的ChannelNet进行训练,一个负责和预测direct channel,一个负责训练和预测cascaded channel
用一些不同信噪比以及噪声数据进行Robust训练
训练样本的标记有两种approach获得(只用关心第一种,逻辑通顺,且效果更好)
训练样本有三个通道,I路Q路和absolute路,说这样效果比单纯IQ好(我持怀疑态度)
信道估计的衡量标准是NMSE
信道建模为SV信道
主要内容
系统模型

- BS有\(M\)根天线
- 同时服务于\(K\)个Users
- IRS有\(L\)个elements
发射信号建模
对第\(k\)th Users发射的信号用\(s_k\in\mathbb{C}\)表示;第\(k\)th用户需求的precoder用\(\textbf{f}_k\in\mathbb{C}^{M\times1}\)表示,且有\(\textbf{F}=[\textbf{f}_1,\cdots,\textbf{f}_K]\in\mathbb{C}^{M\times K}\),所以发射信号为: \[ \begin{align} \bar{s}=\sum\limits_{k=1}^K=\sqrt{\gamma_k}\bar{\textbf{f}}_ks_k\quad\in\mathbb{C}^{M\times1} \label{eqn1} \tag{1} \end{align} \] where \(\bar{\textbf{f}}_k=\frac{\textbf{f}_k}{||\textbf{f}_k||_2}\),\(\gamma_k\)是给\(k\)th User 分配的功率。
值得注意的是:BS是同时给\(K\)个用户发射信号的,这一点与雷达中不同。
接收信号建模
根据3.2小结建模的发射信号,并结合IRS的建模(参考以往文章),得到接收端信号: \[ y_k=(\textbf{h}_{D,k}^\mathrm{H}+\textbf{h}_{A,k}^{\mathrm{H}}\Psi^{\mathrm{H}}\textbf{H}^\mathrm{H})\bar{s}+n_k\label{eqn:2} \tag{2} \] 其中,\(\Psi\)为IRS反射的幅度相位对角阵,\(\Psi=\text{diag}\{\beta_1exp(j\phi_1),\cdots,\beta_Lexp(j\phi_L)\}\),可以控制\(\beta_i\)的大小\(\{0,1\}\)来控制IRS反射与否;\(\textbf{h}_{D,k}^\mathrm{H}\in\mathbb{C}^M\)是 direct channel,\(\textbf{H}^\mathrm{H}\in\mathbb{C}^{M\times L}\)是BS->IRS的信道,\(\textbf{h}_{A,k}^{\mathrm{H}}\in\mathbb{C}^L\)是IRS到User的信道,级联起来有\(\textbf{G}_k=\textbf{H}\cdot\text{diag}\{\textbf{h}_{A,k}\}\in\mathbb{C}^{M\times L}\),则有式\(\ref{eqn:2}\)的级联版本: \[ y_k=(\textbf{h}_{D,k}^\mathrm{H}+\Psi^{\mathrm{H}}\textbf{G}_k^\mathrm{H})\textbf{X}+\textbf{n}_k\label{eqn:3} \tag{3} \] where \(\textbf{X}=[\textbf{x}_1,\cdots,\textbf{x}_P]\in\mathbb{C}^{M\times P}\)为导频信号矩阵,\(P\geq M\)为导频数量。
得到信道标签
有approach 1 和approach 2,但是由于approach 1 比较好理解而且性能更好,只整理approach 1
- 首先,\(\beta_i=0,\forall i=1,\cdots,L\),即turn off 所有element
值得注意的是,这里\(\beta_i\)实际中不可能取0,所以后文也讨论了非0的情况(\(\beta\)是一个极小值)
- 然后,可以由接受到的信号:
\[ \textbf{y}_{D}^{(k)}=\textbf{h}_{D,k}^\mathrm{H}\textbf{X}+\textbf{n}_{D,k} \tag{4} \]
得到\(\textbf{h}_{D,k}\),作为direct channel 的标签
- 再然后,依次打开\(l-th \quad\forall l=1,\cdots,L\) element(每次\(L\)个elements中只有一个被激活),有:
\[ \textbf{y}_{C}^{(k,l)}=(\textbf{h}_{D,k}^\mathrm{H}+\textbf{g}_{k,l}^\mathrm{H})\textbf{X}+\textbf{n}_{k,l} \tag{5} \]
- 由LS算法有:
\[ \hat{\textbf{g}}_{k,l}=(\textbf{y}_C^{(k,l)}\textbf{X}^\mathrm{H}(\textbf{X}\textbf{X}^\mathrm{H})^{-1})\mathrm{H}-\textbf{h}_{D,k} \tag{6} \]
所以有了\(\hat{\textbf{h}}_{D,k}\),就有了\(\hat{\textbf{g}}_{k,l}\),则有\(\hat{G}_k=[\hat{\textbf{g}}_{k,1}\cdots,\hat{\textbf{g}}_{k,L}]\),作为cascaded channel 的标签
准备数据

Supervised Learning

把direct channel数据reshape成了矩阵,方便输入模型;cascaded channel 的数据本来就是一个matrix
实验结果
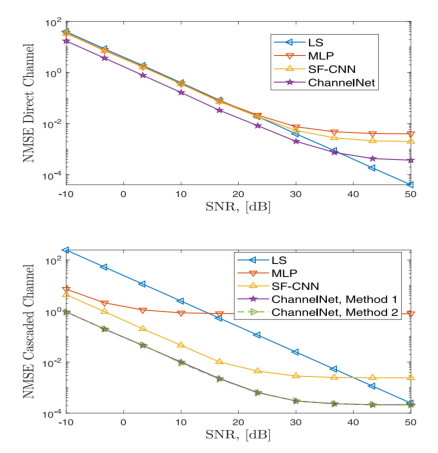
可以看到proposed 结果比LS、MLP好,(因为Direct channel 中,Method 1 和Method 2都是一样的,所以只有一条线),而cascaded channel中,Method 1最好。

给标签(channel Information)加了一定的噪声,以实现泛化 or robustness。

随角度变化(robustness),鲁棒性不错

考虑\(\beta_i\neq0\)这种实际情况,也有不错的表现。