知识储备-压缩感知基础

压缩感知介绍

Compressed Sensing：压缩感知，即在采样过程中实现了数据的压缩

奈奎斯特提出的Nyquist采样定理指出，要想让采样之后的信号完整保留原始信号中的信息，采样频率必须大于信号中最高频率的两倍。（均匀采样）

这是因为时域以$\tau$为间隔采样，频域会以$\tau$为间隔搬移。如果搬移间隔小于$\tau$，就会发生频谱混叠。

但是如果使用非均匀采样，会产生大量不相关（incoherent）的干扰值。随机采样使得频谱不再是整齐地搬移，而是一小部分一小部分胡乱地搬移，频率泄露均匀地分布在整个频域，因而泄漏值都比较小，从而有了恢复的可能。

与图像压缩完全不同，图像压缩是先进行了全采样，再进行压缩（例如变换后丢掉小系数的值）；压缩感知是直接进行亚采样，即在采样的时候已经完成了压缩。

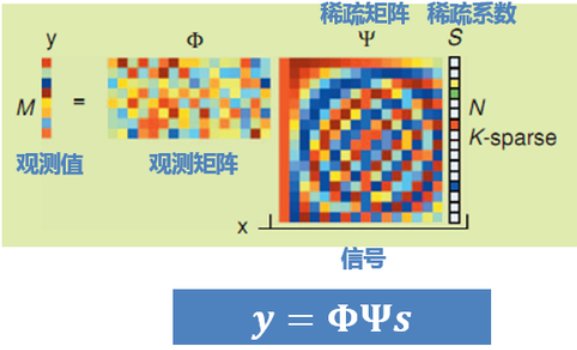
其中，$\textbf{x}=\Psi\textbf{s}$是原始信号，为k-spaese。目的是求解$\textbf{s}$，然后得到$\textbf{x}=\Psi\textbf{s}$

• M=N，很好解
• M<N，根据RIP特性重构

恢复条件

稀疏性

信号需要在某一个变换域具有稀疏性。即大部分值趋于零，只有少量大的非零值。

不相关

Restricted Isometry Property: RIP有限等距性质，即有：

$$\begin{align} (1-\delta_K)\Vert\textbf{u}\Vert_2^2\leq\Vert\Phi\textbf{u}\Vert_2^2\leq(1+\delta_K)\Vert\textbf{u}\Vert_2^2\label{eqn:7} \end{align}$$

其中$\delta_K$称为k-阶受限等距常数(Restricted isometry Constant)。

但是一个矩阵是否满足RIP很难确定，所以Baraniuk证明了等价条件：

RIP的等价条件是观测矩阵和稀疏基不相关

陶哲轩和Candes证明，独立同分布的高斯随机测量矩阵可以称为普适的压缩感知测量矩阵。

如果一个信号在某个变换域是稀疏的，那么就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上，然后通过求解一个优化问题就可以从这些少量的投影中以高概率重构出原信号。

恢复算法

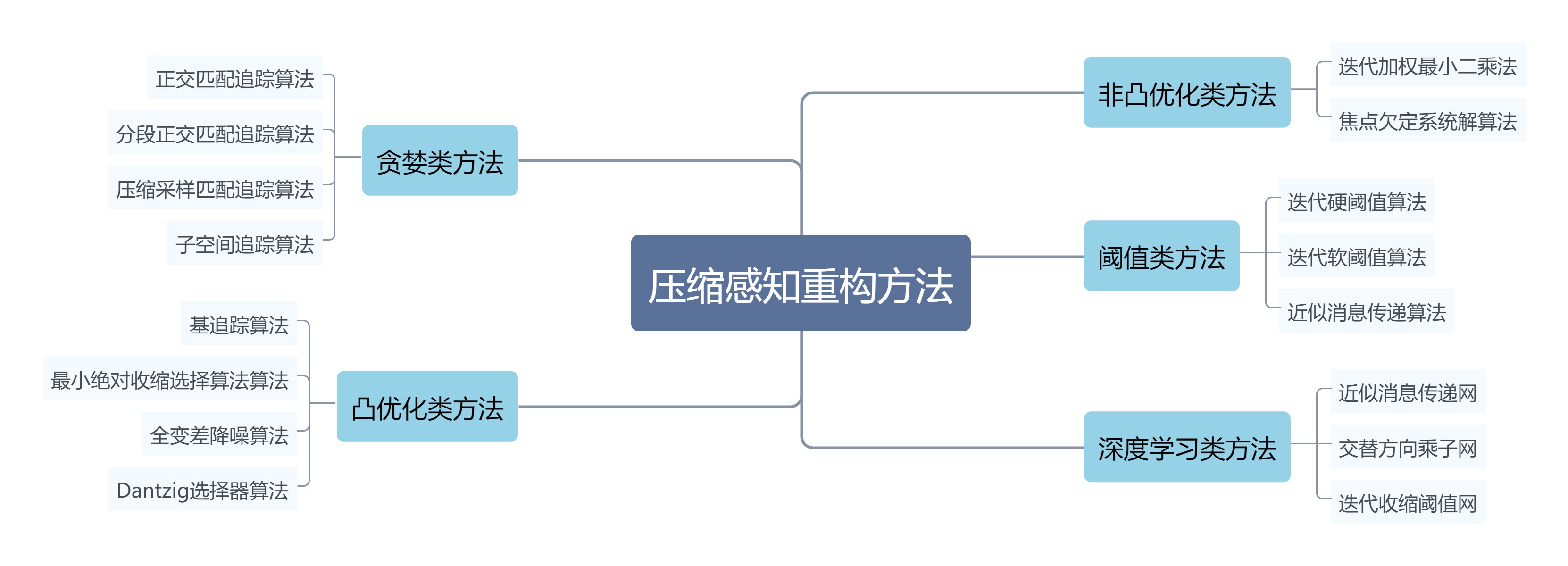
压缩感知信号的重构方法主要包括贪婪算法、凸优化方法、非凸优化方法、阈值方法以及深度学习方法等。其中，贪婪算法主要包括正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)、分段正交匹配追踪算法(Stagewise Orthogonal Matching Pursuit, StOMP)、压缩采样匹配追踪算法(Compressive Sample Matching Pursuit, CoSaMP)、子空间追踪算法(Subspace Pursuit, SP)等；凸优化方法主要包括基追踪算法(Basis Pursuit, BP)、最小绝对收缩与选择算子算法(Least Absolute Shrinkage Selection Operator, LASSO)、全变差降噪算法(Total Variation, TV)等；非凸优化方法主要包括迭代加权最小二乘法(Iteratively Re-Weighted Least Squares, IRWLS)、焦点欠定系统解算法(Focal Underdetermined System Solution, FOCUSS)等；阈值方法主要包括迭代硬阈值算法(Iterative Hard Thresholding, IHT)、迭代软阈值算法(Iterative Soft Thresholding, IST)、近似消息传递算法(Approx-imate Message Passing, AMP)等；随着深度学习技术的发展，一些基于深度学习的压缩感知信号重构算法被提出，主要包括近似消息传递网(Learned Approximate Message Passing Network)、交替方向乘子网(Alternating Direction Method of Multipliers Net, ADMM-Net)、迭代收缩阈值网络(Iterative Shrinkage-Thresholding Algorithm Net, ISTA-Net)等。

OMP

将向量$\textbf{b}$投影到水平面上，其投影为$\textbf{p}$，$a_1,a_2$为水平面的两个线性无关向量，$\textbf{A}=[a_1,a_2]$

投影矩阵：$P=\textbf{A}(\textbf{A}^\mathrm{T}\textbf{A})^{-1}\textbf{A}^\mathrm{T}$

投影$\textbf{p}$为：$\textbf{p}=\textbf{P}\textbf{b}$

MP基本原理：从字典矩阵$\textbf{D}$（也称为过完备原子库中），选择一个与信号$\textbf{y}$（观测值）最匹配的原子(也就是某列)，构建一个稀疏逼近，并求出信号残差，然后继续选择与信号残差最匹配的原子，反复迭代，信号$\textbf{y}$（观测值）可以由这些原子的线性和，再加上最后的残差值来表示。很显然，如果残差值在可以忽略的范围内，则信号$\textbf{y}$（观测值）就是这些原子的线性组合。
OMP改进：OMP 算法是在 MP 算法的基础上进行改进的，其挑选原子的标准和 MP 算法一致，也就是在训练字典$\textbf{D}$里挑选和观测样本$\textbf{y}$最为匹配的字典原子。不相同之处在于：OMP 算法在每一次迭代过程中对所挑选的全部原子先要执行 Schmidt 正交化操作，来确保每一次循环结果都是最优解。使得在同等精度的条件下，OMP 算法的性能更好，其收敛速度也更快。

Reference

https://zhuanlan.zhihu.com/p/22445302

https://blog.csdn.net/tengweitw/article/details/41174555