利用CS进行TDOA

压缩感知和TDOA

目前参考的文章的出发点都在于：并不是说在采样的时候进行压缩，而是先采样，再压缩，再进行传输到TDOA estimator进行恢复和估计。

主要是考虑减少网络通信量，在低速率通信链路上进行数据交换的合适方法。

• TDOA是先采样再压缩
• 不需要重构原始值，只要能保证他们之间的时间关系不被破坏就可以了

Hadamard 观测矩阵（**）

TDOA Estimation With Compressive Sensing Measurements and Hadamard Matrix. Soheil Salari et.al. IEEE Transactions on Aerospace and Electronic Systems, Dec. 2018 (pdf) (Citations 20)

一般的观测矩阵不能用，是因为会破坏时延关系（break up their time-shift relation）

但是Hadamard矩阵可以，并且不会破坏时延关系（但是只能测量2^n的数据维度）

效果很好：

==有点奇怪的地方在于，正常CS是采样和降维同时进行，但是这里是先采样，再进行压缩==

另外值得注意的是：

信号$\times\mathbf{H}_{M\times N}$，进行传输后再$\mathbf{H}^T_{N\times M}$后，虽然信号的幅度完全不同了，但是时间关系还是保持，所以可以直接做相关得到时差估计。

ML Estimation

Maximum Likelihood TDOA Estimation From Compressed Sensing Samples Without Reconstruction. H. Cao et.al. IEEE Signal Processing Letters, May 2017 (pdf) (Citations 22)

首先使用Hadamard矩阵对信号进行采样，然后对CS采样信号（其实我觉得不能成为CS，应该叫做压缩信号/降维信号）直接进行ML Estimation。

$$L(\tau)=-\left\{\sum_{p} \ln |\mathbf{V}(p)|+\sum_{p} \mathbf{R}(p)\right\}$$

Where $\mathbf{R}(p)=\left[\begin{array}{ll} Y_{1}^{*}(p) & Y_{2}^{*}(p) \end{array}\right] \mathbf{V}^{-1}(p)\left[\begin{array}{l} Y_{1}(p) \\ Y_{2}(p) \end{array}\right]$ and $\mathbf{V}(p)=\mathbb{E}\left\{\left[\begin{array}{l} Y_{1}(p) \\ Y_{2}(p) \end{array}\right]\left[Y_{1}^{*}(p) \quad Y_{2}^{*}(p)\right]\right\}$，并且有：

然后由于涉及到统计值，为了方便计算，通过测量值代替统计值，所以设计了算法：

估计参数$\sigma^2$，并且设计：

然后有结果：

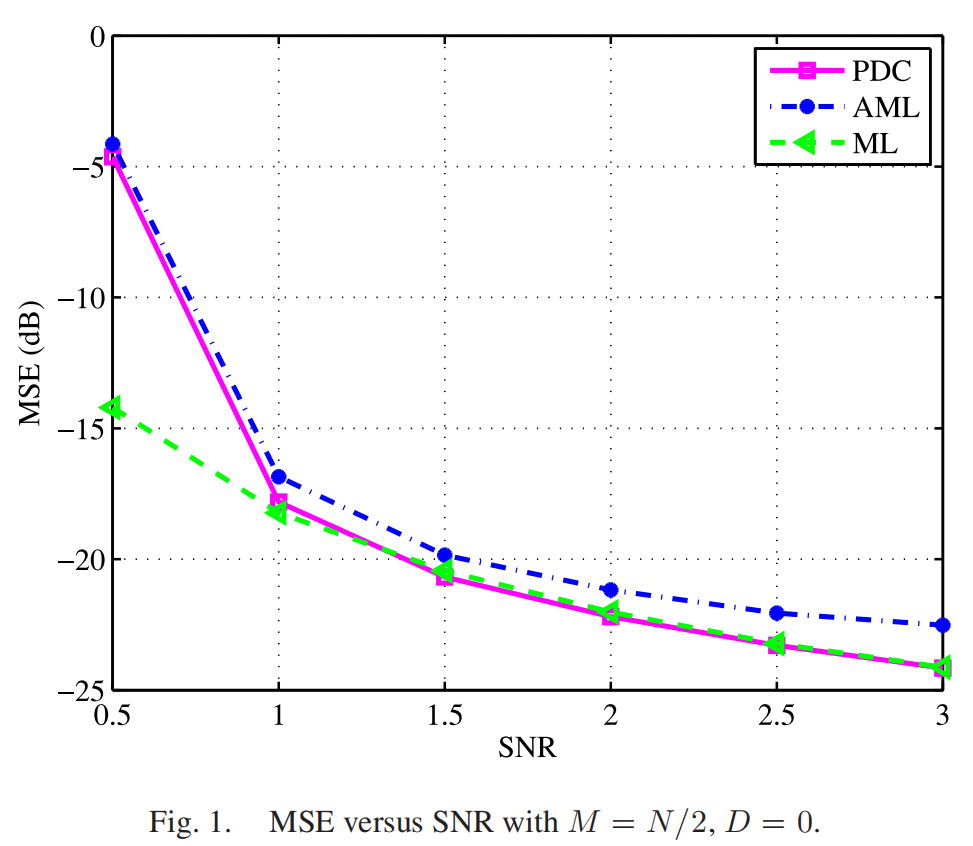
然后推了一下CRLB：

Compressive TDOA Estimation: Cramér–Rao Bound and Incoherent Processing. Hui Cao et.al. IEEE Transactions on Aerospace and Electronic Systems, Aug. 2020 (pdf) (Citations 4)