Active IRS Versus Passive IRS

Wireless Communication Aided by Intelligent Reflecting Surface: Active or Passive?. Changsheng You et.al. IEEE Wireless Communications Letters, Dec. 2021 (pdf) (Citations 9)

Quick Overview

a single antenna access point communicates with a single-antenna user

rate-maximization with passive/active IRS:

  • active IRS should be deployed closer to the RECEIVER with the decreasing amplification power of the active IRS （known in Lemma1）
  • passive IRS is known to be near the transmitter or receiver to minimize the path-loss (known in my-note section 3.2)

optimal the placement:

  • passive IRS outperform active IRS when the number of element is sufficiently large/ the amplification power of the active IRS is too small.(known in my-note section 3.3)
  • optimal placement to maximize the weighted sum-rate of uplink and downlink communications. Passive is more likely to achieve superior rate performance.(known in my-note section 3.4)

Model

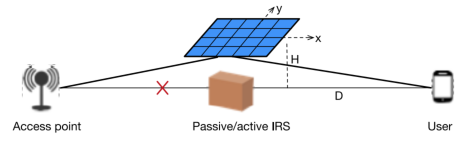
System Model

Main Work

Active IRS

achievable rate =

image-20220613200418754

得到优化目标（P1）：

image-20220613200547459

然后由于（4a）恒成立（是e的指数次项），且（4e）等价形式

（原文这个等式有错误，$$D^2$$没有乘系数1/4）

得到等效的（P2）:

image-20220613200850218

因为信道建模为：

优化目标就是max(SINR)

整理得到优化目标（P3）：

image-20220613201108869

可以得到Lemma1:AP-IRS的距离随的增大而单调递减；随非减。(随的单调递减证明没看懂)

然后有给定的lemma2：

给定:

如果有：

所以由Lemma2可以得到优化目标（P4）：

image-20220613203905971

这就是个高中数学题：

image-20220613211827054

Passive IRS

与active IRS 类似，得到，然后由参考文献给出，对于Passive IRS，，得到：

Active IRS versus Passive IRS

image-20220613213941563

image-20220613213954293

即：

给定较小的，当Active IRS的功率太小或者IRS装配了大量的elements（很大），Passive IRS 往往优于 Active IRS。

maximize the weighted sum-rate of uplink and downlink communications.

对于一个较小的，active IRS 在上行时应该接近AP， 在下行接近User（see Lemma1）。（需要权衡）

而Passive IRS，IRS放置于AP或者User，对于上行/下行都是最佳（因为上行的和下行的最佳是相同的）。（直接最佳）

Simulation

参数设置:

N=400; % number of IRS elements
H=1.5; % IRS altitude
fc =0.75e9; % carrier wave frequency
lambda = 0.4; % wave length 
D = 50; % horizontal distance between AP and User
% Other parameters
PA_dBm = 20; % the power of transmitter (DownLink)
PU_dBm = 15; % the power of receiver (UpLink)
sigma_2_dBm = -80; % noise power from IRS to User
sigma_F_2_dBm = -70; % noise power from AP to IRS 
beta_dB = -30; % reference path loss
% 转换为功率比
PA = 10^((PA_dBm-30)/10);
PU = 10^((PU_dBm-30)/10);
sigma_2 = 10^((sigma_2_dBm-30)/10);
sigma_F_2 = 10^((sigma_F_2_dBm-30)/10);
% beta = (lambda/(4*pi))^2;
beta = 10^(beta_dB/10);

Fig. 2

对比Optimal位置优化和Suboptimal位置优化，证明作者提出的Suboptimal是有效的：

首先是Optimal way，对应于（P3）

image-20220614141413650

function out = optimal_way(PA,PU,sigma_2,sigma_F_2,beta, N, H, D)
out = [];
    for PF_dBm = 0:1:10
        PF = 10^((PF_dBm-30)/10);
        x0 = sqrt(max(0, N*PA*beta/(PF-N*sigma_F_2)-H^2));
        max_obj=0;
        max_indx = 0;
        for xa = x0:1:D % one-dimensional search to find the best placement
            C1 = beta*sigma_F_2;
            C2 = PA*beta*sigma_2/PF;
            C3 = sigma_2*sigma_F_2/PF;
            d_AI_2 = xa^2+H^2;
            d_IU_2 = (D-xa)^2+H^2;
            obj = PA*beta^2*N/(C1*d_AI_2+C2*d_IU_2+C3*d_AI_2*d_IU_2);
            if obj>max_obj
                max_obj = obj;
                max_indx = xa;
            end
        end
        out = [out max_indx];
    end
end

然后是Suboptimal way，对应于（P4）:

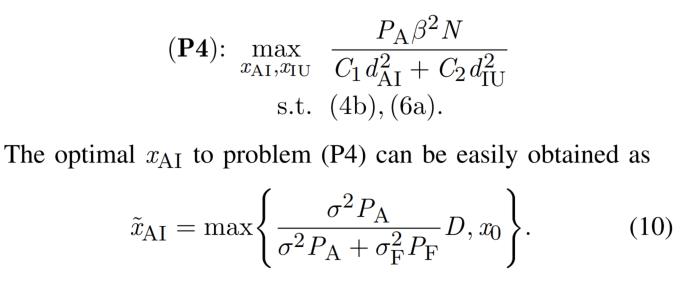
image-20220614141432027

function out = suboptimal_way(PA,PU,sigma_2,sigma_F_2,beta, N, H, D)
    out = [];
    for PF_dBm = 0:1:10
        PF = 10^((PF_dBm-30)/10);
        x0 = sqrt(max(0, N*PA*beta/(PF-N*sigma_F_2)-H^2));
        out = [out max(sigma_2*PA/(sigma_2*PA+sigma_F_2*PF)*D, x0)];
    end
end

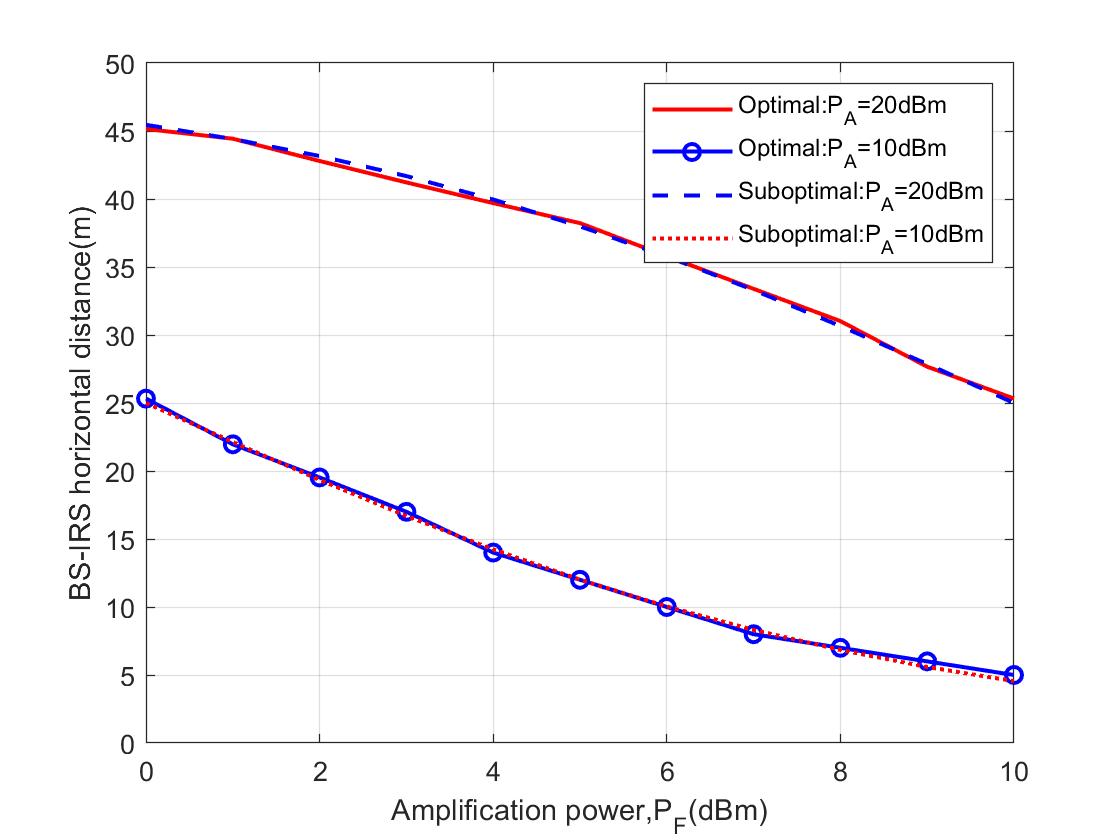
activet_IRS_1_2

Fig. 3

Active IRS的achievable rate需要先算SNR，再由得到。为了方便计算，这里我用Suboptimal优化位置。对应于（eqn.11）

eqn.11

function R_act = ActiveIRS_achievable_rate(PA,PU,sigma_2,sigma_F_2,beta, H, D, PF)
    R_act = [];
    for N=100:10:500
        % 用Suboptimal的位置优化结果求achievable rate
        x0 = sqrt(max(0, N*PA*beta/(PF-N*sigma_F_2)-H^2));
        threshold = sigma_2*PA*D/(sigma_2*PA+sigma_F_2*PF);
        if x0<=threshold
            SNR_act = N*beta/(D^2)*(PA/sigma_F_2+PF/sigma_2);
        else
            disp('2')%发现一个问题，所有的x0都小于threshold
            C1 = beta*sigma_F_2;
            C2 = PA*beta*sigma_2/PF;
            SNR_act = PA*beta^2*N/(C1*x0^2+C2*(D-x0)^2);
        end
        R_act = [R_act log2(1+SNR_act)];
    end
end

Passive IRS同理：

eqn.15

function R_pas = PassiveIRS_achievable_rate(PA,PU,sigma_2,sigma_F_2,beta, H, D)
    R_pas = [];
    for N=100:10:500
        SNR_pas = PA*beta^2*N^2/(H^2*(H^2+D^2)*sigma_2);
        R_pas = [R_pas log2(1+SNR_pas)];
    end
end

activet_IRS_1_3

Fig. 4

计算weighted sum-rate，意味存在两个分配问题：

  • IRS位置
  • 上行、下行分配的时间（我是这么理解$w^{(UL)}$和$w^{(DL)}$）

对于Active IRS，对应（P6）：

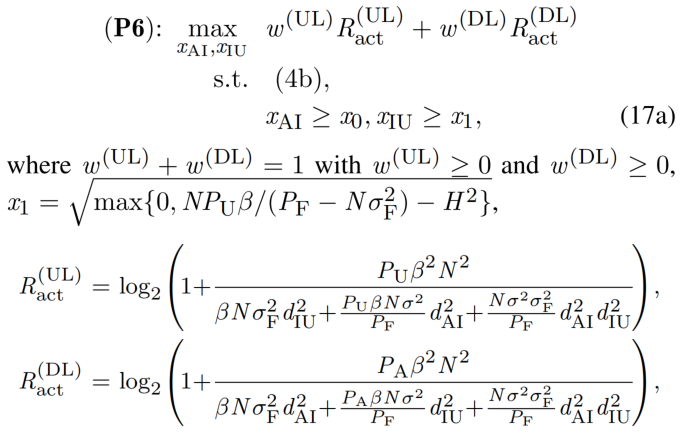
image-20220614142439139

function out = ActiveIRS_Weighted_Sum_rate(PA,PU,sigma_2,sigma_F_2,beta, N, H, D, PF)
    out = [];
    for w_dl = 0:0.02:1
        w_ul = 1-w_dl;
        max_obj = 0;
        for xa=0:1:D
            d_AI_2 = xa^2+H^2;
            d_IU_2 = (D-xa)^2+H^2;
            R_act_UL = log2(1+PU*beta^2*N^2/(beta*N*sigma_F_2*d_IU_2+PU*beta*N*sigma_2/PF*d_AI_2+N*sigma_2*sigma_F_2/PF*d_AI_2*d_IU_2));
            R_act_DL = log2(1+PA*beta^2*N^2/(beta*N*sigma_F_2*d_AI_2+PA*beta*N*sigma_2/PF*d_IU_2+N*sigma_2*sigma_F_2/PF*d_AI_2*d_IU_2));
            obj = w_ul*R_act_UL+w_dl*R_act_DL;
            max_obj = max(max_obj, obj);
        end
        out = [out , max_obj];
    end
end

对于Passive IRS，对应（P7）：

function out = PassiveIRS_Weighted_Sum_rate(PA,PU,sigma_2,sigma_F_2,beta, N, H, D, PF)
    out = [];
    for w_dl = 0:0.02:1
        w_ul = 1-w_dl;
        R_obj = w_ul*log2(1+PU*beta^2*N^2/(H^2*(D^2+H^2)*sigma_2))+w_dl*log2(1+PA*beta^2*N^2/(H^2*(D^2+H^2)*sigma_2));
        out = [out R_obj];
    end
end

activet_IRS_1_4

Fig. 5（结果和论文中有一定差异）

考虑对weighted sum-rate 的影响，Active IRS：

w_dl = 0.5;
w_ul = 1-w_dl;
out = [];
for H = 1.5:0.5:10
    max_obj = 0;
    for xa=0:1:D
        d_AI_2 = xa^2+H^2;
        d_IU_2 = (D-xa)^2+H^2;
        R_act_UL = log2(1+PU*beta^2*N^2/(beta*N*sigma_F_2*d_IU_2+PU*beta*N*sigma_2/PF*d_AI_2+N*sigma_2*sigma_F_2/PF*d_AI_2*d_IU_2));
        R_act_DL = log2(1+PA*beta^2*N^2/(beta*N*sigma_F_2*d_AI_2+PA*beta*N*sigma_2/PF*d_IU_2+N*sigma_2*sigma_F_2/PF*d_AI_2*d_IU_2));
        obj = w_ul*R_act_UL+w_dl*R_act_DL;
        max_obj = max(max_obj, obj);
    end
    out = [out , max_obj];
end

Passive IRS：

out = [];
for H = 1.5:0.5:10
    R_obj = w_ul*log2(1+PU*beta^2*N^2/(H^2*(D^2+H^2)*sigma_2))+w_dl*log2(1+PA*beta^2*N^2/(H^2*(D^2+H^2)*sigma_2));
    out = [out, R_obj];
end

activet_IRS_1_5

Question

complex channel gain到底指什么?

Passive IRS 为什么x=D/x=0?