合作IRS-一个IRS拆分为两个

Cooperative Double-IRS Aided Communication: Beamforming Design and Power Scaling. Yitao Han et.al. IEEE Wireless Communications Letters, Aug. 2020 (pdf) (Citations 37)

Quick Overview

BS单天线、USER单天线 对IRS每一个element单元进行建模

作者讨论了将一个拥有\(K\)个elements的IRS分解为两个分别拥有\(K_1\)和\(K_2\)(且\(K_1+K_2=K\))的IRS1和IRS2

• 当\(K\)足够大的时候，分割为两个IRS性能比一个IRS(有\(K\)个elements)要好。是因为其虽然受到了一共三段path-loss（BS-IRS1 IRS1-IRS2 IRS2-USER）但是其性能随\(K^4\)增长

• 为了简化IRS1-IRS2的channel，作者利用了IRS1-IRS2 channel 的rank-one性质，即IRS1如果对准IRS2中任意一个element，则IRS2中其他elements收到相同增益。

Main work

System model

假设上图所示的模型。则有\(\mathbf{t}\in\mathbb{C}^{K_1\times1}\),\(\mathbf{S}\in\mathbb{C}^{K_1\times K_2}\),\(\mathbf{r}^T\in\mathbb{C}^{1\times K_2}\)，两个IRS的反射系数为\(\Phi_1\)和\(\Phi_2\)，则信道为： \[ h=\mathbf{r}^T\Phi_2\mathbf{S}\Phi_1\mathbf{t} \]

作者引入了三维坐标系，对每个IRS element进行位置建模

将上述三个信道建模为LoS，有：

然后利用\(\mathbf{S}\)的Rank-one性质，简化\(\mathbf{S}\)为：

这意味着只要知道位置信息，就可以对IRS1-IRS2的channel进行建模

Design of Joint Passive Beamforming

取\(\Phi_1\)的元素\(\phi_{1,k_1}\)为：

\[ \phi_{1, k_{1}}=\left(\frac{\left(\mathbf{g}_{1}\right)_{k_{1}}(\mathbf{t})_{k_{1}}}{\left|(\mathbf{t})_{k_{1}}\right|}\right)^{*}, \quad k_{1} \in \mathcal{K}_{1} \]

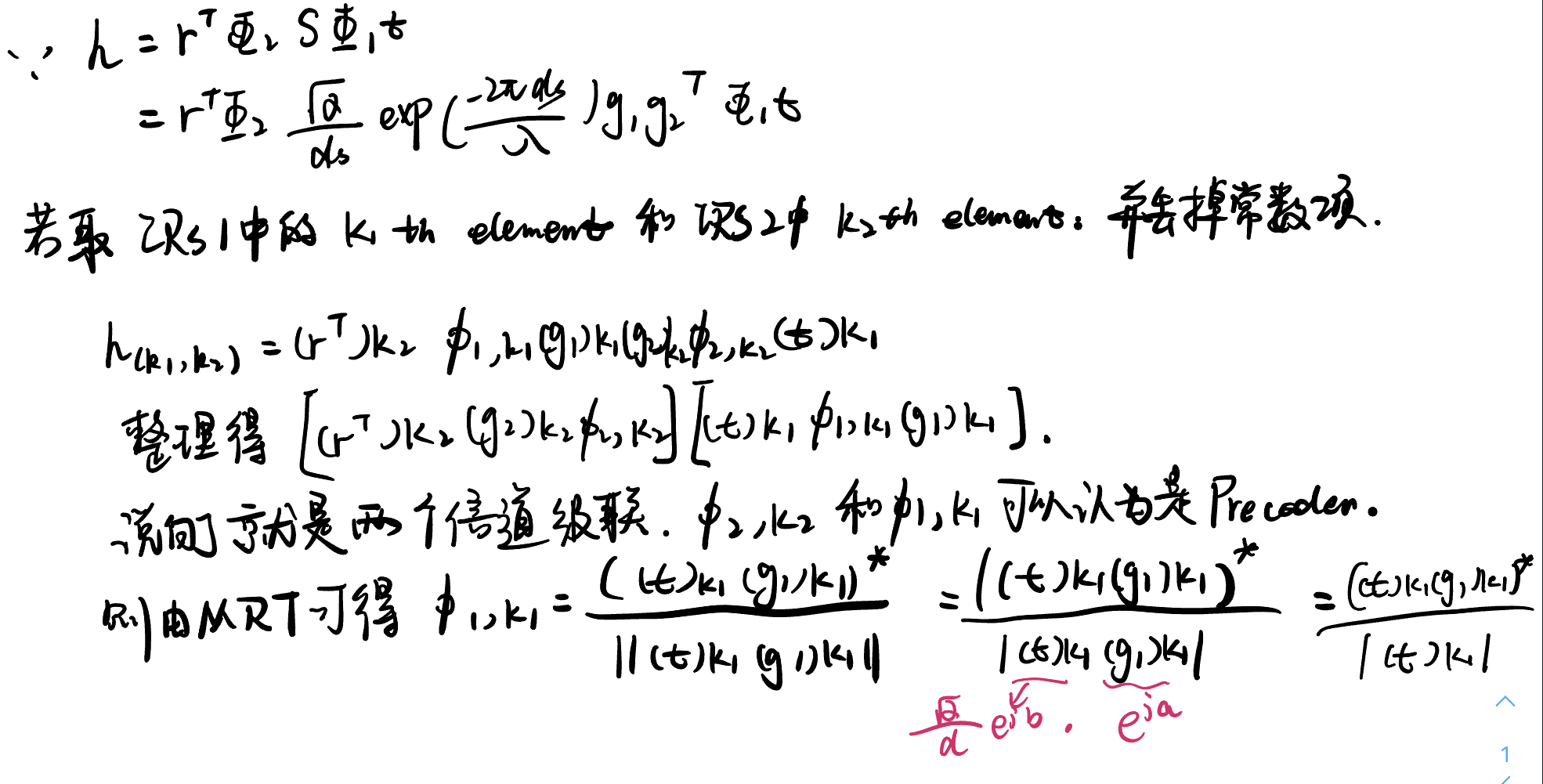
对于\(\Phi_2\)中的元素\(\phi_{2,k_2}\)同理。

此时的接收端： \[ |h|^{2}=\left|\mathbf{r}^{T} \mathbf{\Phi}_{2} \mathbf{S} \boldsymbol{\Phi}_{1} \mathbf{t}\right|^{2} \approx \frac{\alpha^{3}}{\left(d_{\mathbf{r}} d_{\mathbf{S}} d_{\mathbf{t}}\right)^{2}}\left(K_{1} K_{2}\right)^{2} \]

Simulation

我只仿真了2.2节中推导的近似表达式的结果，因为实际的结果需要对每个IRS element建模，有点复杂，而且不知道作者怎么将IRS elements进行排布的。所以这里就没有仿真。

clc;clear;close all;
u1 = [0.87, 0.50, 0]; % location of BS
u2 = [13, 92.50, 0]; % location of USER
v1 = [0, 0, 0]; % element(0, 0) on IRS1
v2 = [0, 100, 0]; % element(0, 0) on IRS2
dt = caculate_dis_3d(u1, v1); % distance between BS and IRS1
ds = caculate_dis_3d(v1, v2); % distance between IRS1 and IRS2
dr = caculate_dis_3d(v2, u2); % distance between IRS2 and USER
n1a = [0, 0, 1];
n1b = [sqrt(3)/2, -1/2, 0];

% proof that IRS 1 faces towards the BS
n1a*u1.'
n1b*u1.' % 垂直于n1a

n2a = [sqrt(3)/2, 1/2, 0];
n2b = [0, 0, 1];

f = 5e9;
lambda = 3e8/f;

alpha_dB = -46;% reference_path_loss_dB
alpha = 10^(alpha_dB/10);
l = lambda/2;
Pt_dBm = 43;
Pt = 10^((Pt_dBm-30)/10); % W
sigma_dBm = -60;
sigma = 10^((sigma_dBm-30)/10);

K = 1600;

SNR_coop = [];
for K1 = 70:10:1530
    SNR_coop = [SNR_coop Pt*alpha^3/(ds*dr*dt)^2*K1^2*(K-K1)^2/sigma];
end
plot(70:10:1530, 10*log10(SNR_coop))
ylim([-8 18])
hold on;

SNR_single =  Pt*alpha^2/(dr*ds)^2*K^2/sigma;
plot(70:10:1530, 10*log10(SNR_single)*ones(length(SNR_coop)), 'r--');
hold on;


K = 800;

SNR_coop_2 = [];
for K1 = 70:10:800-70
    SNR_coop_2 = [SNR_coop_2 Pt*alpha^3/(ds*dr*dt)^2*K1^2*(K-K1)^2/sigma];
end
plot(70:10:800-70, 10*log10(SNR_coop_2))
ylim([-8 18])
hold on;

SNR_single_2 =  Pt*alpha^2/(dr*ds)^2*K^2/sigma;
plot(70:10:800-70, 10*log10(SNR_single_2)*ones(length(SNR_coop_2)), 'r--');
hold off;
grid on;

需要用到一个function：

function dis = caculate_dis_3d(loc1, loc2)
    dis = sqrt((loc1(1)-loc2(1))^2+(loc1(2)-loc2(2))^2+(loc1(3)-loc2(3))^2);
end

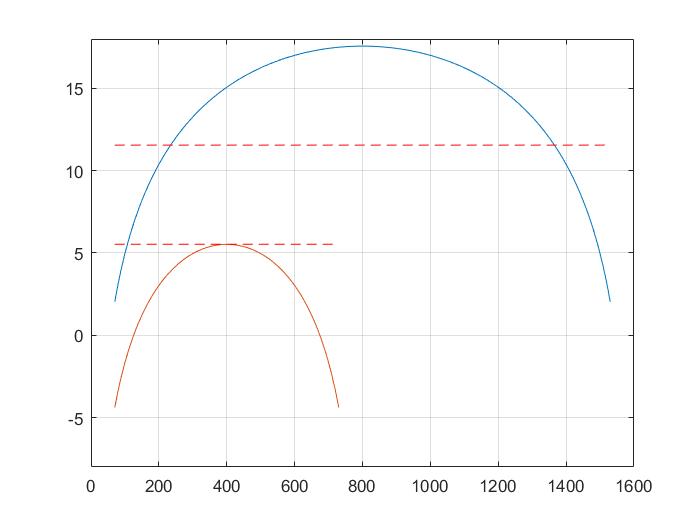
结果和作者文中的结果有一定的出入，但是在相对的增益上是相同的：

• 800 elements 和1600 elements 的benchmark case之间差约6dB
• 800 elements 和1600 elements 的two IRS cooperation case之间差约12dB

说明仿真问题应该是在某些稀疏上进行了整体的缩放。

Question

• 作者提出这个模型，前提条件是inner IRS信道是rank-one的。这个rank-one到底决定了\(\textbf{S}\)推导的哪一步？

if IRS 1 beams towards one element on IRS 2, the rest elements on IRS 2 can enjoy the same power gain

• 这种对每一个element建模的方法是否是主流？有没有必要？