Metasurface/IRS 调频（一）

High-Efficiency Synthesizer for Spatial Waves Based on Space-Time-Coding Digital Metasurface. Jun Yan Dai et.al. LASER & PHOTONICS REVIEWS, 2020 (pdf) (Citations 24)

Quick Overview

两个关键点

• 实现从基波、+1-st、-1-st 谐波的抑制或转换（如果能很好地抑制不想要的谐波，则转换效率应该很大。理想中最大为100%，即完全抑制不需要的谐波）
• 实现在这些转换的谐波上进行波束赋形，使波束指向某一特定方向

提出的方法可以同时进行频率转换和beam shaping。

高次谐波的产生主要与discrete phase states相关。

谐波转换

给出入射信号和反射信号的表达式，假设入射单频信号$E_{\mathrm{i}}(t)=e^{j2\pi f_0t}$：

$$E_{\mathrm{r}}(t)=E_{\mathrm{i}}(t) \cdot A(t) \mathrm{e}^{j \varphi(t)}$$

令$\Gamma(t)=A(t) e^{j \varphi(t)}$且：

$$\varphi(t)=\varphi_0+p \cdot \bmod (t, T)$$

其中$T$为调制周期，$\varphi_0$为初相。假设$A(t)=A_0$为定值。

因为$\varphi(t)$为周期函数，所以可以通过傅里叶级数展开：

$$E_r(t)=A_0 \cdot \mathrm{e}^{\left[\varphi_0+p \cdot \bmod (t, T)\right]} \cdot \mathrm{e}^{j 2 \pi f_0 t}=\sum_{k=-\infty}^{+\infty} a_k \mathrm{e}^{j k \frac{2 \pi}{T} t} \mathrm{e}^{j 2 \pi f_0 t}$$

且：

$$a_k=\left|A_0 \operatorname{sinc}\left(\frac{p T}{2}-k \pi\right)\right| \mathrm{e}^{j\left[\varphi_0+\frac{p T}{2}-k \pi+\bmod \left(\left\lfloor\frac{p T}{2 \pi}-k \mid, 2\right) \cdot \pi+\varepsilon(2 k \pi-p T) \cdot \pi\right]\right.}$$

当$pT = 2m\pi$，有：

$$a_k=\left\{\begin{array}{cc} A_0 \mathrm{e}^{j \varphi_0}, & k=m \\ 0, & k \neq m \end{array}\right.$$

所以可以通过选择适当的$p$来控制需要的谐波，并且转换率可以达到$100\%$

从上图也可以看到，当$p$取不同的值时，留存有不同的谐波，例如在$p=2\pi/T$，仅有$k=m=1$次谐波有幅度为1，其余谐波幅度都未0。

然后，考虑discrete phase带来的量化误差（quantization error）。选取$p=2\pi/T$，即仅保留+1-st谐波，结果如下：

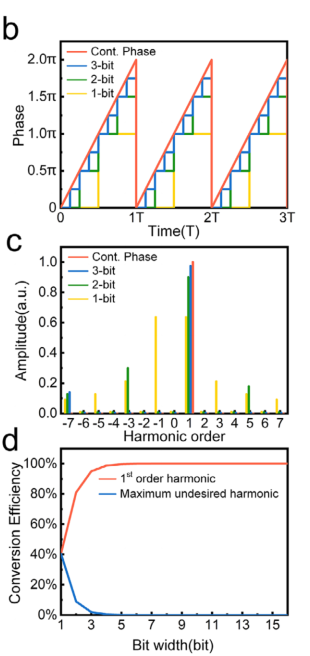
看起来3-bit就可以实现很好地谐波抑制。

Beam shaping

假设metasurface以列为单位，每一列的反射矩阵为$\Gamma^n(t)$，即只考虑二维ULA。则远场天线方向图的表达式：

$$f(\theta, t)=\sum_{n=1}^N E^n(\theta) \Gamma^n(t) e^{j \frac{2 \pi f_0}{c}(n-1) d \sin \theta}$$

其中$E^n(\theta)\approx \cos\theta$（代表定向天线的方向因子）。则谐波$f_0+k/T$的方向图为：

$$F_k(\theta)=\sum_{n=1}^N E^n(\theta) a_k^n \mathrm{e}^{j \frac{2 \pi\left(f_0+k / T\right)}{c}(n-1) d \sin \theta}$$

进一步，仅有$m$阶的能保留下来$a^n_m\neq0$，则：

$$F_m(\theta)=\sum_{n=1}^N E^n(\theta) A_0 \mathrm{e}^{j\left[\frac{2 \pi\left(f_0+m / T\right)}{c}(n-1) d \sin \theta+\varphi_0\right]}$$

==一般而言，通过调整相位可以改变波束指向，但是这里的相位已经用于谐波生成了，不适合再用于调整波束指向==

所以作者认为可以通过反射单元引入时延来实现相位的调整。

这个说法有点奇怪，为什么不直接再调相位？时延的相位差最后还是叠加在整体上的，和直接调整应该没啥区别。

指向方向：

实际硬件

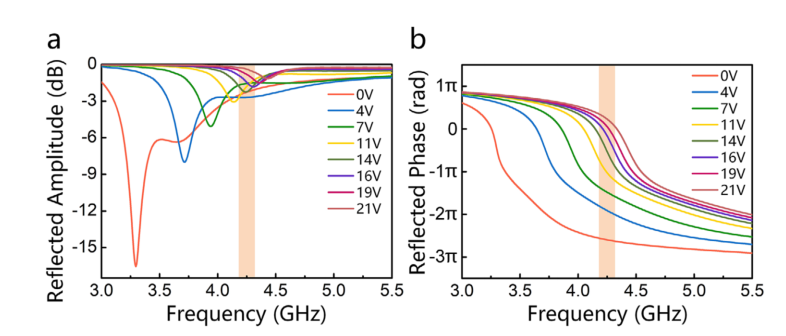
通过给不同的偏置电压，可以实现不同的相位，同时也有不同的幅度相应（希望幅度相应是平稳的）。

谐波$\Delta f$越大， 泄露越多。$\varphi_0$和$p$还可以决定是正阶谐波还是负阶谐波