无限制采样-Unlimited Sampling

Date: 2022.11.15 20:01
Author: Joffrey LC

---

On Unlimited Sampling and Reconstruction. Ayush Bhandari et.al. IEEE Transactions on Signal Processing, 2021 (pdf) (Citations 16)

Quick Overview

那天健完身和王佬吃饭的时候，聊到了一种unlimited sampling，感觉非常适合应用到数能上。先找了一篇文章看一下，作为以后可能的拓展方向。

---

主要的思想是，在一般的ADCs中，会存在限幅的问题。可以使用==self-reset ADCs==来避免。

但是self-reset ADCs又引入了新的问题：self-reset ADCs等于是对信号一直取模，但是==怎么恢复==是难点。

• 推导了完美恢复的条件
• 需要的采样密度独立于限幅电压（意思是电压再大，都可以恢复），只与信号的带宽相关
• 分析了抗噪性能（因为恢复的阶级性，所以对噪声有一定鲁棒性）

ADCs

一般的ADC，存在限幅$[-\lambda,\lambda]$。

意味着采样信息损耗：

---

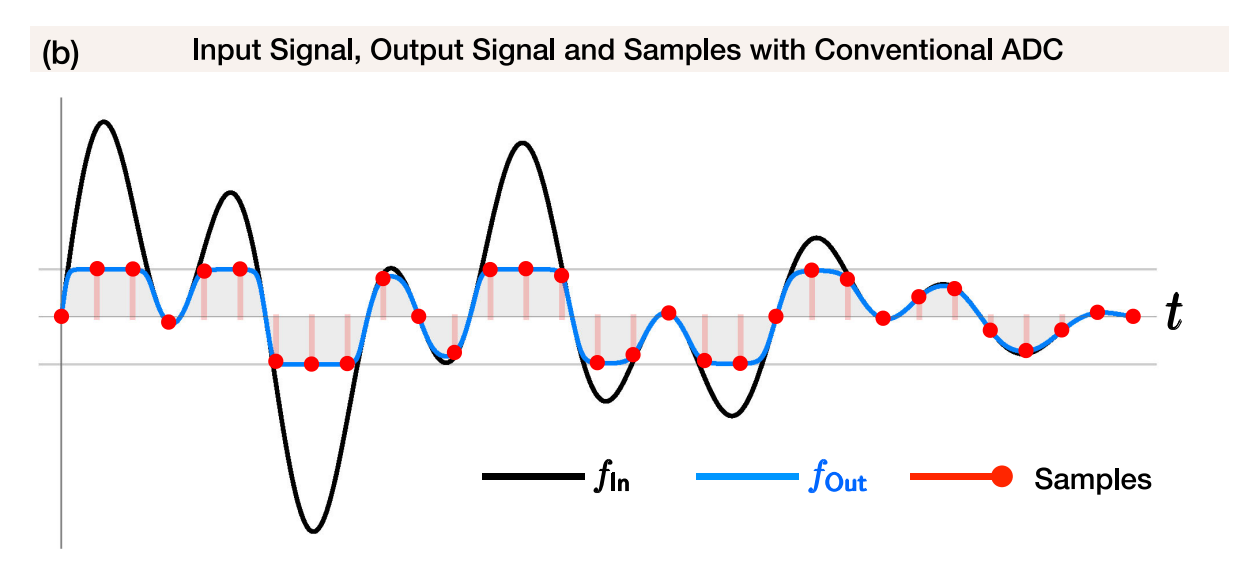
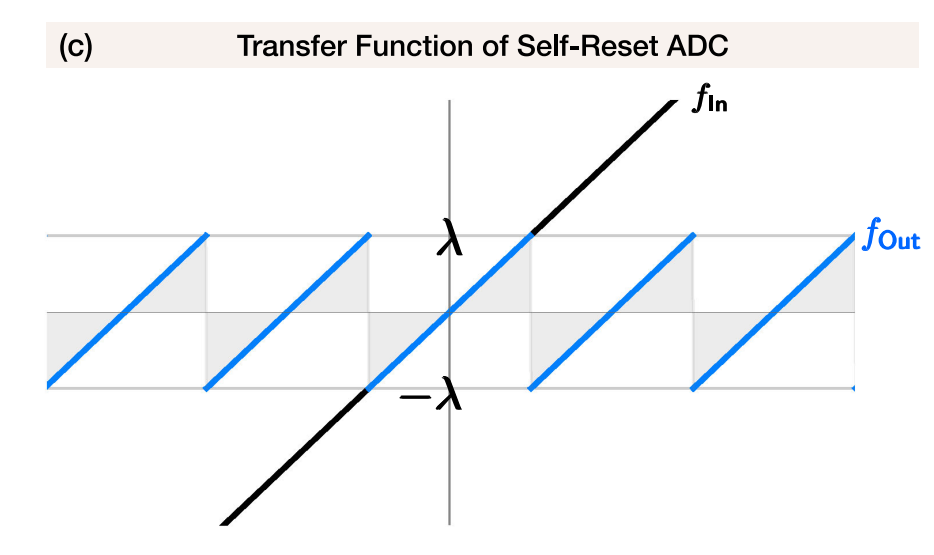
self-reset ADCs会对信号取模，即将信号进行折叠：

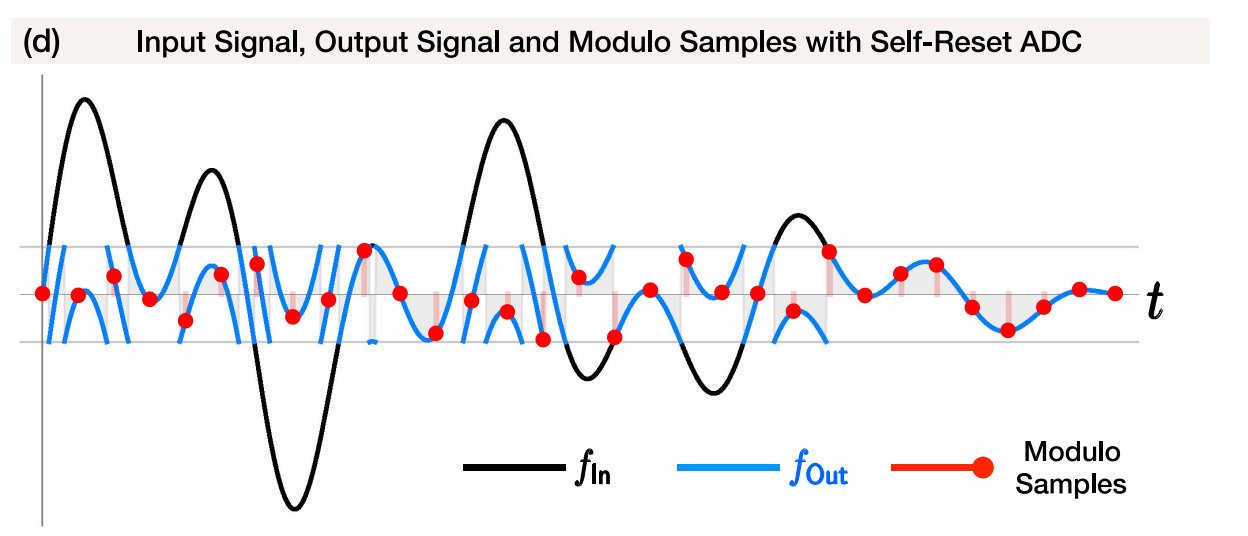
但是恢复困难。==这就是作者研究的重点==

对平滑信号的截断导致突变和非平滑，对应于信号中的高频失真

算法

实际上就是解决残差的计算。注意残差是只有几个量化等级的，意味着计算出来的结果可以就近往上靠（强制对齐），以获得较强的鲁棒性。

作者的方法是通过采样值倒推折叠次数的方法。

TO BE CONTINUE …

CODE

Github code

def reconstruction_unlimited_sampling(y, lamb, beta, T, omega):
    try: 
        J = int(beta*6/lamb)
        N = math.ceil((math.log(lamb)-math.log(beta))/(math.log(T*omega*math.e)))
        delta_n_y = np.diff(y, N)
        m_delta_n_y = np.mod(delta_n_y, [2*lamb])
        delta_n_epsilon = m_delta_n_y -delta_n_y
        s_i_1 = delta_n_epsilon
        for i in range(N-1):
            s_i = s(s_i_1, lamb)
            k_i = k(np.cumsum(np.cumsum(s_i_1)), beta, J)
            s_i += 2*lamb*k_i
            s_i_1 = s_i
    except:
        pass


def s(y, lamb):
    return 2*lamb*np.ceil(np.floor(np.cumsum(y)/lamb)/2)


def k(s_i, beta, J):
    return math.floor((s_i[1]-s_i[J+1])/(12*beta)+1/2)