mymathtools

X服从高斯分布，求\(\sin X/\cos X\)的均值高阶矩

https://zhuanlan.zhihu.com/p/515334478

\(1+\cos x+\cdots+\cos(N-1)x\)

对单独一项\(\cos nx\)，乘\(\sin\frac{x}{2}\)，由积化和差得： \[ \sin\frac{x}{2}\cos nx=\frac{1}{2}(\sin(\frac{x}{2})+\sin(\frac{x}{2}-nx)) \] 得求和项\(\cos x+\cos2x+\cdots+\cos(N-1)x\)为： \[ \frac{-\sin(\frac{x}{2})+\sin(\frac{x}{2}+(N-1)x)}{2\sin(\frac{x}{2})} \] 同理，\(\sin x+\sin2x+\cdots+\sin(N-1)x\)为： \[ \frac{\cos(\frac{x}{2})-\cos(\frac{x}{2}+(N-1)x)}{2\sin(\frac{x}{2})} \] matlab实现版本：

https://www.zhihu.com/zvideo/1405113965265899520

IRS计算变型

Robust Beamforming and Phase Shift Design for IRS-Enhanced Multi-User MISO Downlink Communication. Jun Wang et.al. ICC 2020 - 2020 IEEE International Conference on Communications (ICC), June 2020 (pdf) (Citations 17) \[ \begin{align} &|\mathbf{h}^\mathrm{H}\boldsymbol{\Theta}\mathbf{G}\mathbf{w}|^2\\ =&|\text{diag}(\mathbf{\Theta})^\mathrm{T}\text{diag}(\mathbf{h^\mathrm{H}})\mathbf{G}\mathbf{w}|^2 \end{align} \] 记\(\mathbf{v}=\text{diag}(\mathbf{\Theta})\)，有： $$ \[\begin{align} &|\mathbf{v}^\mathrm{T}\left(\mathbf{H}+\Delta\mathbf{H}\right)\mathbf{w}|^2\\ =&\mathbf{v}^\mathrm{T}(\mathbf{H}+\Delta\mathbf{H})\mathbf{w}\mathbf{w}^\mathrm{H}(\mathbf{H}+\Delta\mathbf{H})^\mathrm{H}\mathbf{v}^\mathrm{*} \\ =&\text{vec}^\mathrm{H}(\Delta\mathbf{H})\mathbf{Q}\text{vec}(\Delta\mathbf{H})+2\Re\{\mathbf{q}^\mathrm{H}\text{vec}(\Delta\mathbf{H})\}+c \end{align}\] \[ 其中： \] =()=()^* \ =()\ c=()^() $$ 验证代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
clc;clear;close all
%% Initial Parameters
warning('off')
% max_err_all = 0/180*pi;
thre_energy = 5e-5;
loc_IRS = [0, 0, 0];
loc_user = [5*sqrt(2), -5*sqrt(2), 0];
loc_BS = [0, sqrt(2), sqrt(2)];

Ke = 1; % num of user, only one user 2m
M = 4 ; % num of transmitter antennas 10m
N = 100; % num of IRS elements

r1 = sqrt(sum((loc_BS-loc_IRS).^2)); % distance between PB to IRS
r2 = sqrt(sum((loc_user-loc_IRS).^2)); % distance between IRS to User

reference_attenuation = -30; % reference attenuation at 1 m.

kappa_h = 5; % Rician factor of IRS to User channel 
kappa_G = 5; % Rician factor of PB to IRS channel 

% path_loss_PB2IRS = channel_path_loss(r1, 2.2, reference_attenuation); % path loss of PB to IRS channel 
% path_loss_IRS2Ues = channel_path_loss(r2, 2.2, reference_attenuation); % path loss of IRS to User channel
path_loss_PB2IRS = 1;
path_loss_IRS2Ues = 1;
%% channel generation 
G_bar = generate_channel_simple(M, N, -pi/2+pi*rand, -pi/2+pi*rand, -pi/2+pi*rand);
G_hat =sqrt(1/2)*(randn(N,M)+1j*randn(N,M));
G = sqrt(kappa_G/(1+kappa_G))*G_bar+ sqrt(1/(1+kappa_G))*G_hat;
G =sqrt(path_loss_PB2IRS)*G;

GG_bar = sqrt(path_loss_PB2IRS)*sqrt(kappa_G/(1+kappa_G))*G_bar;
GG_hat = sqrt(path_loss_PB2IRS)*sqrt(1/(1+kappa_G))*G_hat;;

h_bar = generate_channel_simple(Ke, N, -pi/2+pi*rand, -pi/2+pi*rand, -pi/2+pi*rand);
h_hat = sqrt(1/2)*(randn(N,Ke)+1j*randn(N,Ke));

h = sqrt(kappa_h/(1+kappa_h))*h_bar+sqrt(1/(1+kappa_h))*h_hat;
h = sqrt(path_loss_IRS2Ues)*h;

hh_bar = sqrt(path_loss_IRS2Ues)*sqrt(kappa_h/(1+kappa_h))*h_bar;
hh_hat = sqrt(path_loss_IRS2Ues)*sqrt(1/(1+kappa_h))*h_hat;

w = randn(M, 1)+1j*randn(M, 1);
w = w./norm(w);
% trace(w*w')
Theta = diag(exp(1j*randn(1, N)));

H = diag(hh_bar)'*GG_bar;
d_H = diag(hh_bar)'*GG_hat+diag(hh_hat)'*GG_hat+diag(hh_hat)'*GG_bar; %

v= diag(Theta);
abs(h'*Theta*G*w)^2
abs(v.'*(H+d_H)*w)^2

real(v.'*(H+d_H)*w*w'*(H+d_H)'*conj(v))

Q = kron(conj(w)*w.', conj(v)*v.');
real(myvec(H+d_H)'*Q*myvec(H+d_H))

q = Q*myvec(H);
c = myvec(H)'*Q*myvec(H);
real(myvec(d_H)'*Q*myvec(d_H)+2*real(myvec(d_H)'*q)+c)
real(myvec(d_H)'*Q*myvec(d_H)+2*real(q'*myvec(d_H))+c)

还有带SINR的变型，具体可以参见：==\(\mathbf{Q}\),\(\mathbf{q}\),\(c\),==的取值会发生变化。

A Framework of Robust Transmission Design for IRS-Aided MISO Communications With Imperfect Cascaded Channels. Gui Zhou et.al. IEEE Transactions on Signal Processing, 2020 (pdf) (Citations 135)

有： \[ \mathbf{1}_M^T \mathbf{T} \overline{\mathbf{W}} \mathbf{T}^H \mathbf{1}_M=\mathbf{1}_M^T \boldsymbol{\Pi} \boldsymbol{\Xi} \boldsymbol{\Pi}^H \mathbf{1}_M \] 其中\(\mathbf{W}=\mathbf{w}\mathbf{w}^\mathrm{H}\)，\(\mathbf{T}=\operatorname{diag}\left(\hat{\mathbf{g}}_{\mathbf{I} 2 \mathrm{U}}\right) \boldsymbol{\Theta} \mathbf{G}_{\mathrm{B} 2 \mathrm{I}}\)，\(\boldsymbol{\Xi}=\text{diag}(\mathbf{\Theta)}\text{diag}(\mathbf{\Theta)}^\mathrm{H}\)，\(\boldsymbol{\Pi}=\operatorname{diag}\left(\operatorname{diag}\left(\hat{\mathbf{g}}_{\mathrm{I} 2 \mathrm{U}}\right)\mathbf{G}_{\mathrm{B} 2 \mathrm{I}} \mathbf{w}\right)\)

验证代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
clc;clear;close all;

loc_IRS = [0, 0, 0];
loc_user = [5*sqrt(2), -5*sqrt(2), 0];
loc_BS = [0, sqrt(2), sqrt(2)];

Ke = 1; % num of user, only one user 2m
M = 4 ; % num of transmitter antennas 10m
N = 36; % num of IRS elements


r1 = sqrt(sum((loc_BS-loc_IRS).^2)); % distance between PB to IRS
r2 = sqrt(sum((loc_user-loc_IRS).^2)); % distance between IRS to User

reference_attenuation = -30; % reference attenuation at 1 m.

kappa_h = 3; % Rician factor of IRS to User channel 
kappa_G = 3;

path_loss_PB2IRS = channel_path_loss(r1, 2.2, reference_attenuation); % path loss of PB to IRS channel 
path_loss_IRS2Ues = channel_path_loss(r2, 2.2, reference_attenuation); % path loss of IRS to User channel



%% channel generation 
G_AOA1 = pi/2;
G_AOA2 = pi/4;
G_AOD = -pi/4;
G_bar = generate_channel_simple(M, N, G_AOA1, G_AOA2, G_AOD);
G_hat = sqrt(1/2)*(randn(N,M)+1j*randn(N,M));
G =sqrt(path_loss_PB2IRS)*(sqrt(kappa_G/(1+kappa_G))*G_bar+sqrt(1/(1+kappa_G))*G_hat);

h_AOA1 = pi/4;
h_AOA2 = pi/2;
h_AOD = -pi/2+pi*rand;
h_bar = generate_channel_simple(Ke, N, h_AOA1, h_AOA2, h_AOD);
h_hat = sqrt(1/2)*(randn(N,Ke)+1j*randn(N,Ke));
h = sqrt(path_loss_IRS2Ues)*(sqrt(kappa_h/(1+kappa_h))*h_bar+sqrt(1/(1+kappa_h))*h_hat);

w0 = 100*exp(1j*randn(M, 1)); % inits
w_best = w0;

Theta0 = diag(exp(1j*randn(N, 1))); % init
Theta_best = Theta0;

T = diag(h)*Theta_best*G;
W = w_best*w_best';
A = ones(1,N)*T*W*T'*ones(N, 1);

II = diag(diag(h)*G*w_best);
XI = diag(Theta_best)*diag(Theta_best)';
B =ones(1,N)*II*XI*II'*ones(N, 1);

Bernstein-Type Inequality

A Framework of Robust Transmission Design for IRS-Aided MISO Communications With Imperfect Cascaded Channels. Gui Zhou et.al. IEEE Transactions on Signal Processing, 2020 (pdf) (Citations 135)

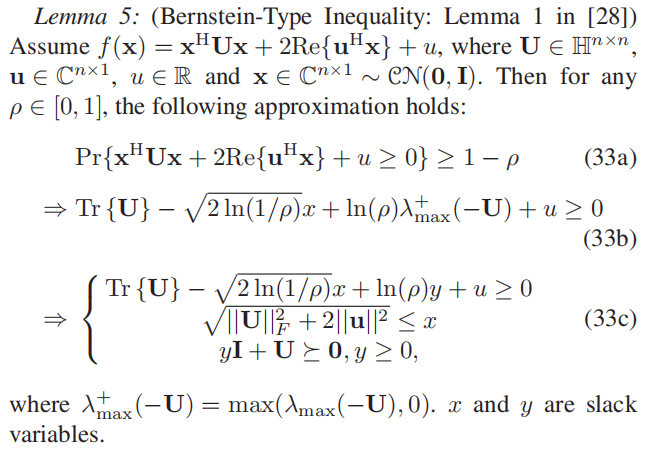
image-20221230120036399

General S-Procdure

A Framework of Robust Transmission Design for IRS-Aided MISO Communications With Imperfect Cascaded Channels. Gui Zhou et.al. IEEE Transactions on Signal Processing, 2020 (pdf) (Citations 135)

image-20221230120136566

moment-matching

关键词：矩匹配，PDF，CDF，逆CDF，逆累计分布函数

思想很简单，就是用Gamma分布近似一个复杂分布。由于Gamma分布的参数只与均值和方差有关，这意味着我们只要求出待求随机变量的均值和方差，就可以拟合其PDF。

1
2
3
beta = myapprox_mean/myapprox_var/(path_loss_IRS2Ues*path_loss_PB2IRS); % scaler parameter
alpha = myapprox_mean^2/myapprox_var; % shape parameter
inv_X = gaminv(P_out, alpha, 1/beta)

其中gaminv是Gamma分布的逆累计分布函数。alpha是 Gamma分布的shape parameter， beta是Gamma分布的scaler parameter。

AOA/AOD

关键词：LoS，视距信道，面阵，IRS

网上的对IRS面阵的空间向量的建模都是错的，这里我整理一下。

明确俯仰角/方位角

参考《现代数字信号处理及其应用》Page291 和《阵列信号处理及matlab实现》Page 42-43

image-20230325105446079

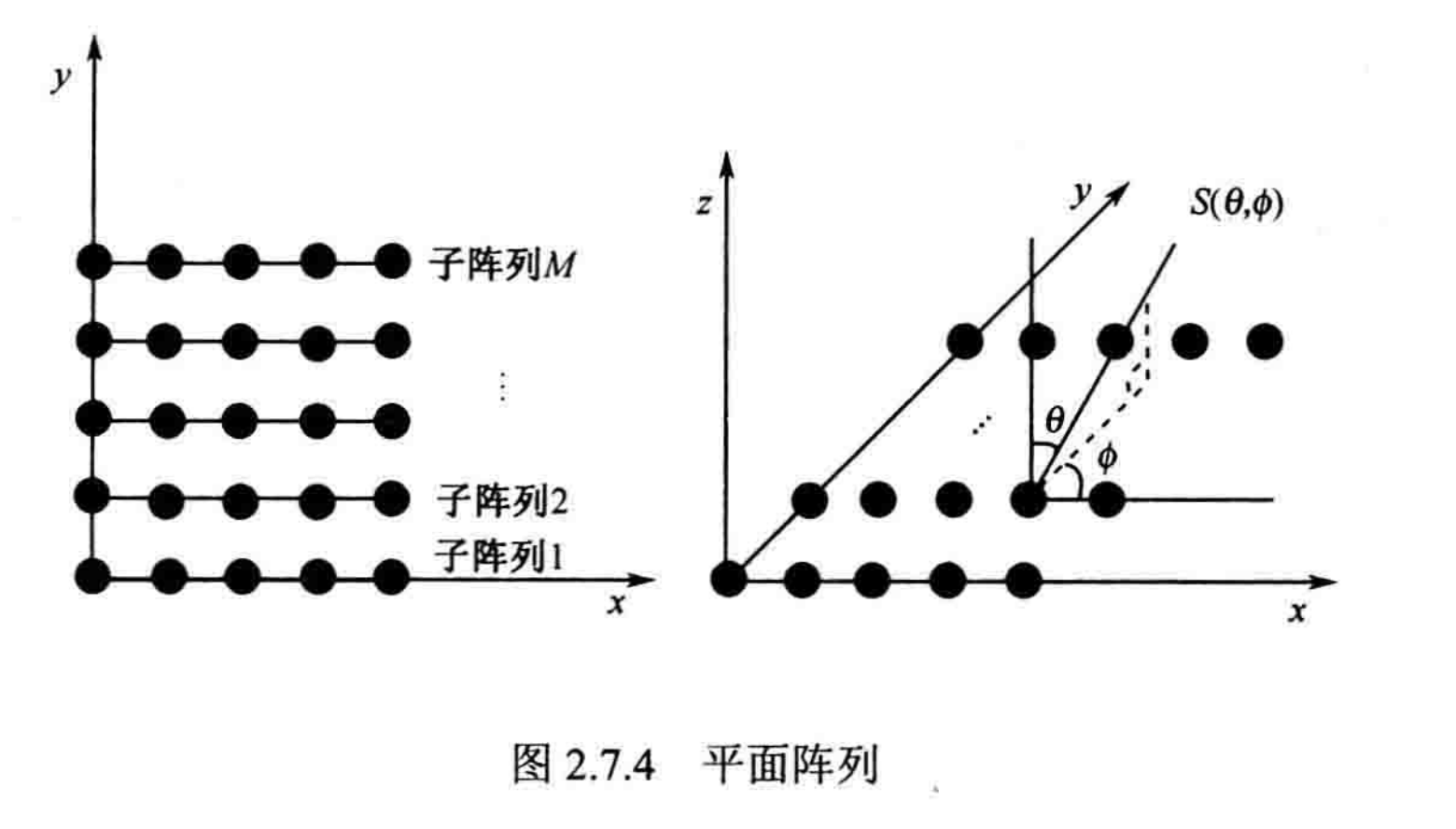
image-20230325105438173

==明确以L阵的俯仰角和方位角进行建模。==

明确角度后进行分析

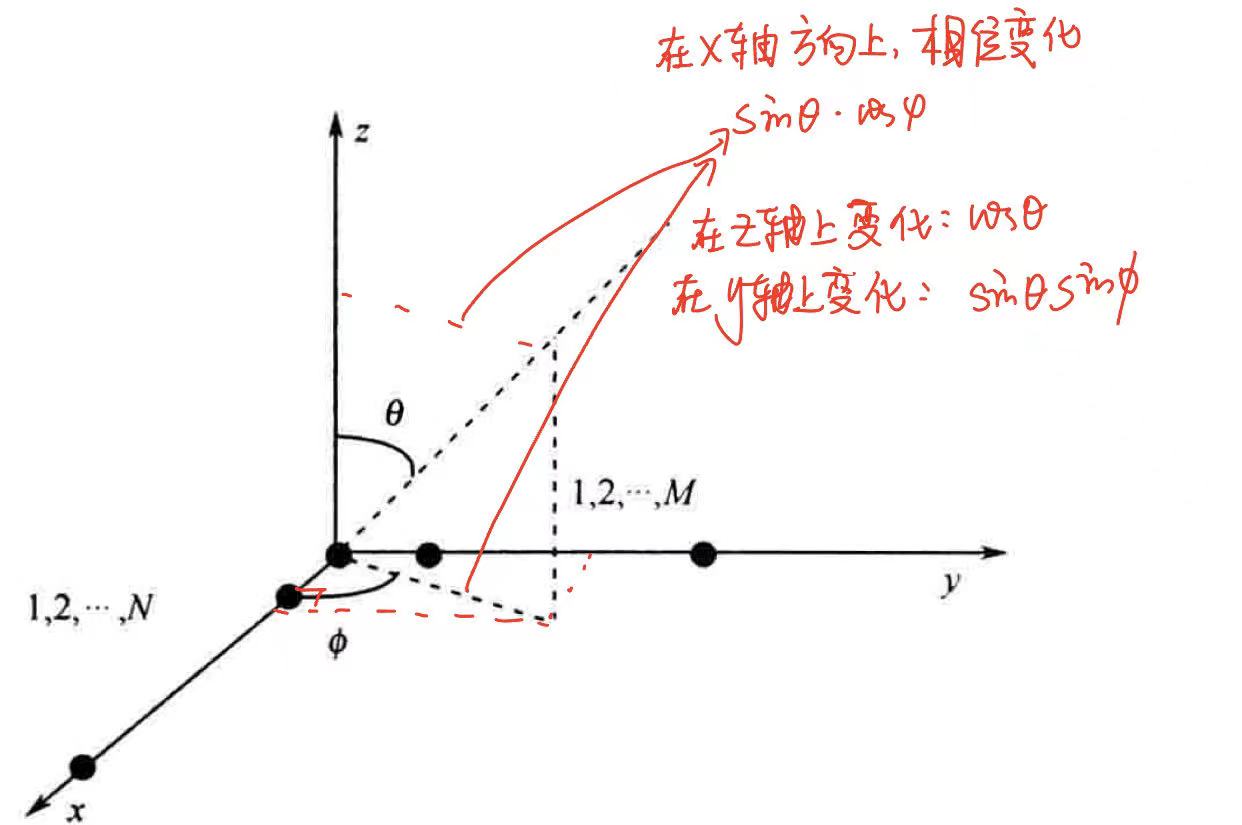
c33ad9009804428e4f106271504bd30

所以对于我常用的模型，

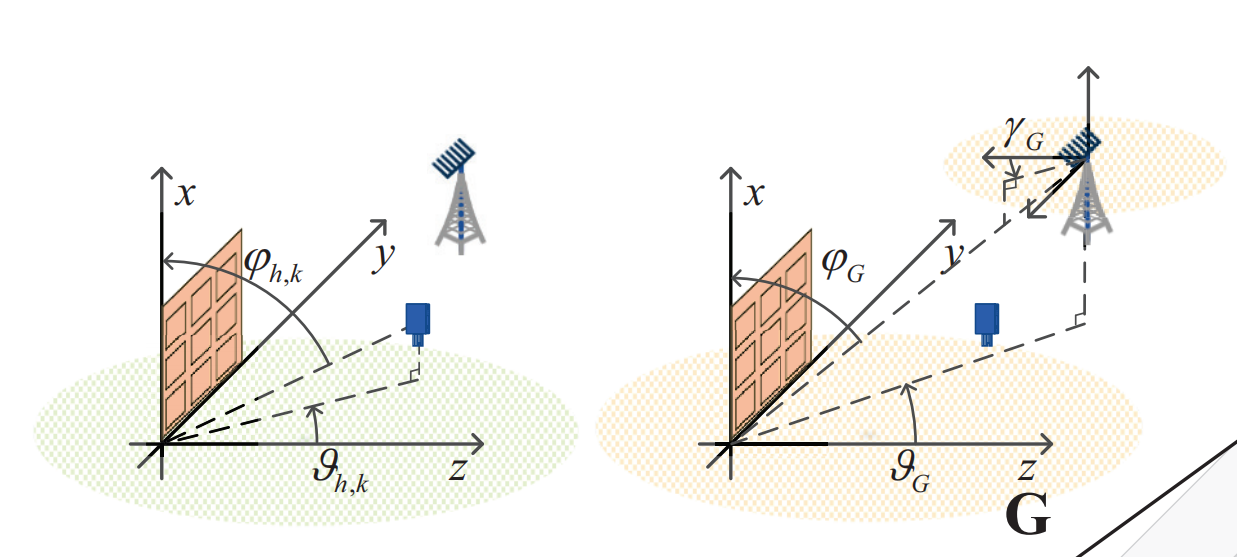
image-20230325110217963

有： \[ u_{G}\triangleq 2\pi d\cos\varphi_{G} /\lambda=\pi\cos\varphi_{G}\\ v_{G}\triangleq \pi\sin\varphi_{G}\sin\vartheta_{G}\\ z_{G}\triangleq \pi\sin\gamma_{G} \]

天线的近场和远场

详细信息参见：微信公众号

主要结论 ==判断是否远场，是与天线尺寸和工作波长相关的：== \[ r\geq\frac{2d^2}{\lambda} \] 其中\(d\)为阵元之间的间隔，\(\lambda\)为波长，\(r\)为距离。

Study field
#Mathmatical
mymathtools
https://lcjoffrey.top/2022/11/28/mymathtools/
作者
Joffrey
发布于
2022年11月28日
更新于
2023年3月25日
许可协议