IRS + Tracking Self-Sensing Scheme

Target Sensing With Intelligent Reflecting Surface: Architecture and Performance. Xiaodan Shao et.al. IEEE Journal on Selected Areas in Communications, July 2022 (pdf) (Citations 15)

Quick Overview

• 设计了一种单独发射基站，IRS（反射+接收信号和处理），目标的结构。与传统的单基站感知定位（收发两种天线or全双工形式）相比，没有干扰（干扰很小）
• 用MUSIC估计角度，最小化其MSE很难，==所以等价于最大化接收端（IRS controller）的接收平均信号功率==（有参考文献证明）
• 基于离散傅里叶变换（DFT）的IRS被动反射是最优的。（主要是进行全向波束的扫描，对我而言不应该是这样）
• 推导了CRB

其实这篇文章很简单，写的很复杂。

System Model

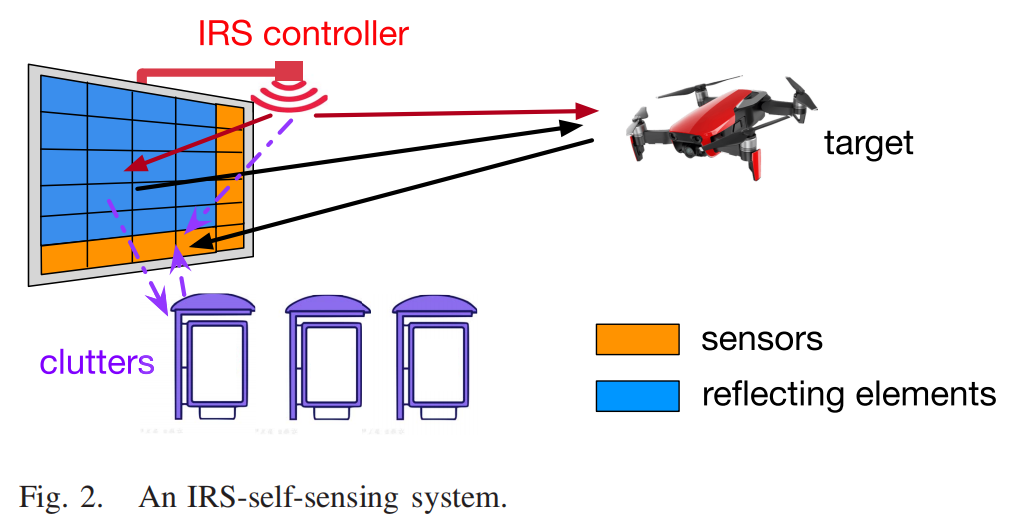
• IRS controller 单天线
• target回波也等于是只收到了一个RCS（雷达截面积）的损耗

Details

所以实际接收到的信号为：

$$\begin{aligned} & \mathbf{y}_0[t]=(\mathbf{g}_{\mathrm{r}}[t]+\mathbf{g}_{\mathrm{d}}+\underbrace{\sum_{\ell=1}^L\left(\mathbf{g}_{\mathrm{r}, I_{\ell}}[t]+\mathbf{g}_{\mathrm{d}, I_{\ell}}\right)+\mathbf{h}_{\mathrm{CS}}}_{\text {background channel }}) x[t]+\mathbf{z}_0[t], \quad t \in \mathcal{T} \end{aligned}$$

其中的background channel其实是想要去掉的。所以作者设计了offline和online。

offline阶段：

$$\mathbf{y}_{\mathrm{int}}(\boldsymbol{\varphi})=(\underbrace{\sum_{\ell=1}^L\left(\mathbf{g}_{\mathrm{r}, I_{\ell}}(\boldsymbol{\varphi})+\mathbf{g}_{\mathrm{d}, I_{\ell}}\right)+\mathbf{h}_{\mathrm{CS}}}_{\mathbf{g}_{\mathrm{int}}(\boldsymbol{\varphi}) \text { : background channel }}) x+\tilde{\mathbf{z}},$$

假设没有target，对环境背景噪声进行估计，注意这里是有个$\tilde{\mathbf{z}}\sim\mathcal{CN}(0,\sigma_0^2)$。

online阶段：

这个时候由接受到的信号减去background channel，就得到了期望信号。==但是得注意，此时的噪声$\mathbf{z}[t]\sim\mathcal{CN}(0,\sigma^2)$，此时$\sigma^2=2\sigma^2_0$，因为两个noise的减法，方差相加==。

最后把信号写成了

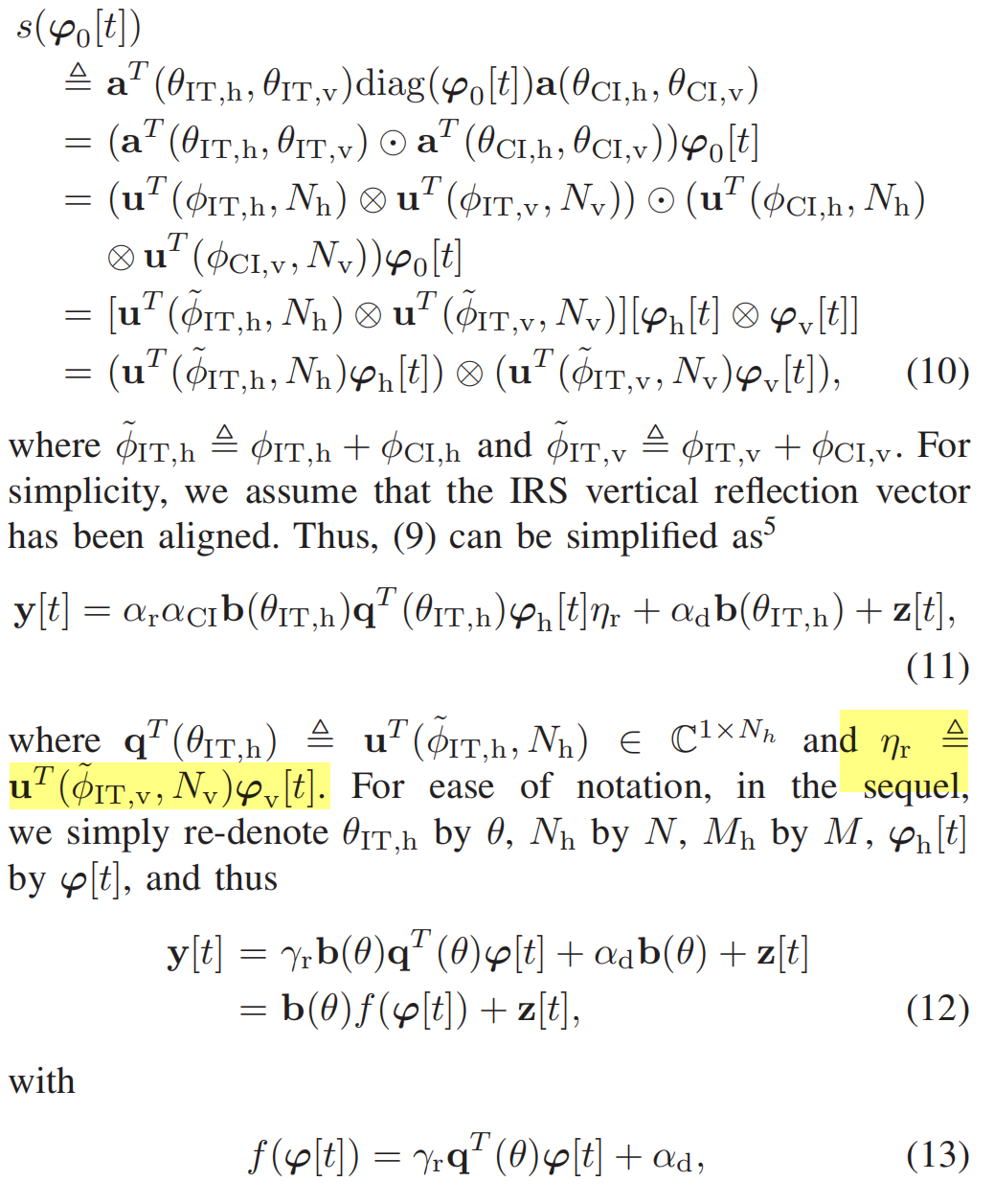
因为作者只假设了一个二维的角度估计，所以只有一个水平的角度需要估计，然后竖直方向的角度认为是固定的（常量），所以把常量写到一起，整理为（13）的形式，最后拿这个做MUSIC：

主体就结束了。

More

• 然后做了一个优化问题，得到最佳的IRS反射向量。（在没有任何先验信息的前提下，最大化接收功率的期望，最后得到的结果为一个全向扫描的Phase shift vector）

• 求解了CRB