Approximating DFT matrix through Stacked Intelligent Metasurfaces
Two-Dimensional Direction-of-Arrival Estimation Using Stacked Intelligent Metasurfaces
Quick Overview
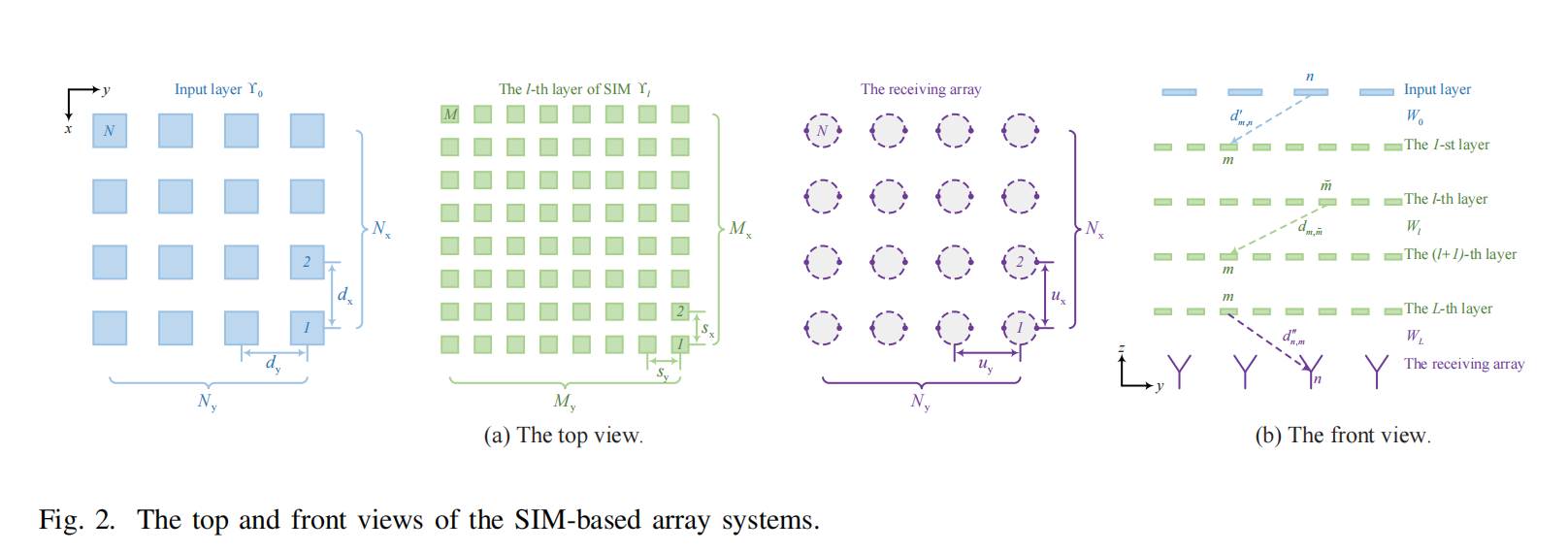
Stacked Intelligent Metasurfaces: 多个RIS堆叠,densely integrating multiple metasurface layers
An advanced SIM in front of the receiver array automatically carries out the 2D discrete Fourier transform (DFT) as the incident waves propagate through it.
- configure the phase shift pattern in the zeroth layer of the SIM to generate a set of 2D DFT matrices associated with orthogonal spatial frequency bins to improve the DOA estimation accuracy further.
(没怎么懂)
evaluate the performance of the proposed SIM-based DOA estimator by deriving a tight upper bound for the mean square error (MSE)
- 空中计算
SIM的四个关键参数
- The thickness TSIM of the SIM;(总共厚度,总厚度/层数=间隔)
- The number L of metasurface layers; (多少层)
- The number M of meta-atoms per layer; (每层多少个element)
- The spacing between elements in the x and y directions, namely sx and sy; 单元间隔
传统的DOA估计方案,受到瑞利准则限定,入射角度需要大于波束宽度才能被区分。
基本原理

充当ANN/fully connected neural network.
在最初的文章[1]中,作者通过5块SIM来进行手写数字识别
- 第一个超表面层充当DAC,灰度转换。其余四层是fully connected neural network.
- 本文将SIM集成到接收端,在接收端进行自然地计算(2D-DFT)从而使得能量在最后一层的某个点汇集,通过检测不同接收器探头的能量水平(每个探头对应一个独特的 DOA),我们可以从具有最强能量的探头读取信号的方向。
- 自然计算,没有任何延迟
- Adjust the phase shift in the zeroth layer of the SIM for each snapshot to generate a set of 2D DFT matrices having mutually orthogonal spatial frequency bins to improve the accuracy of estimation.
System model
SIM model
- 每一层的信道建模为:
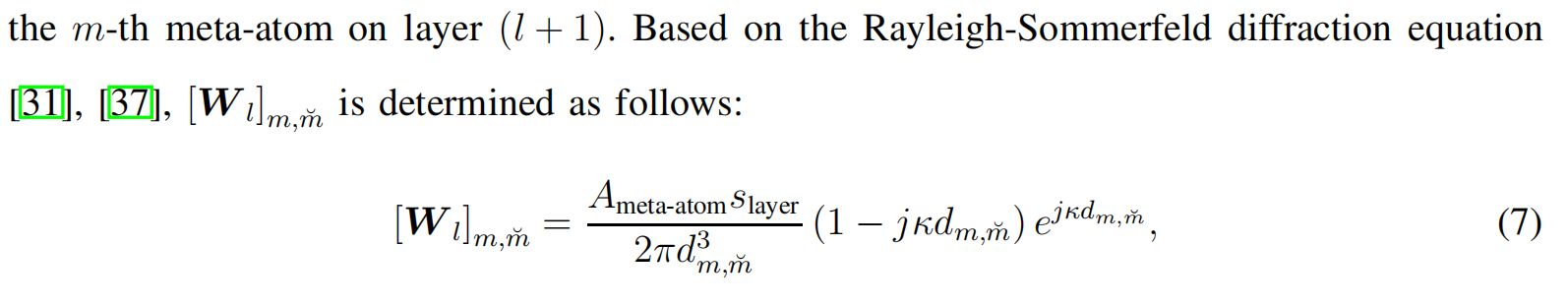
值得注意的是,输入层和输出层单元数不是那么多,距离计算方式有点变化。
记\(\boldsymbol{v}_0=\left[v_{0,1}, v_{0,2}, \cdots, v_{0, N}\right]^T \in \mathbb{C}^{N \times 1}\)和\(\boldsymbol{\Upsilon}_0=\operatorname{diag}\left(\boldsymbol{v}_0\right) \in \mathbb{C}^{N \times N}\)分别为 complex-valued transmission coefficient vector and the corresponding matrix for the input layer (i.e., the zeroth layer),所以整个系统模型被建模为: \[ \boldsymbol{G}=\boldsymbol{W}_L \boldsymbol{\Upsilon}_L \boldsymbol{W}_{L-1} \cdots \boldsymbol{W}_2 \Upsilon_2 \boldsymbol{W}_1 \boldsymbol{\Upsilon}_1 \boldsymbol{W}_0 \]
Received model
Received model和正常的RIS类似: \[ \boldsymbol{r}=\sqrt{\varrho} \boldsymbol{G} \Upsilon_0 \boldsymbol{x}+\boldsymbol{u}=\sqrt{\varrho} \boldsymbol{G} \Upsilon_0 \boldsymbol{a}\left(\psi_{\mathbf{x}}, \psi_{\mathrm{y}}\right) s+\boldsymbol{u} \]
- 虽然\(\mathbf{G}\)包含大量矩阵乘法,但是这些矩阵乘法都是在传播过程中自动发生, 即以光速进行运算的。
Problem and Solution
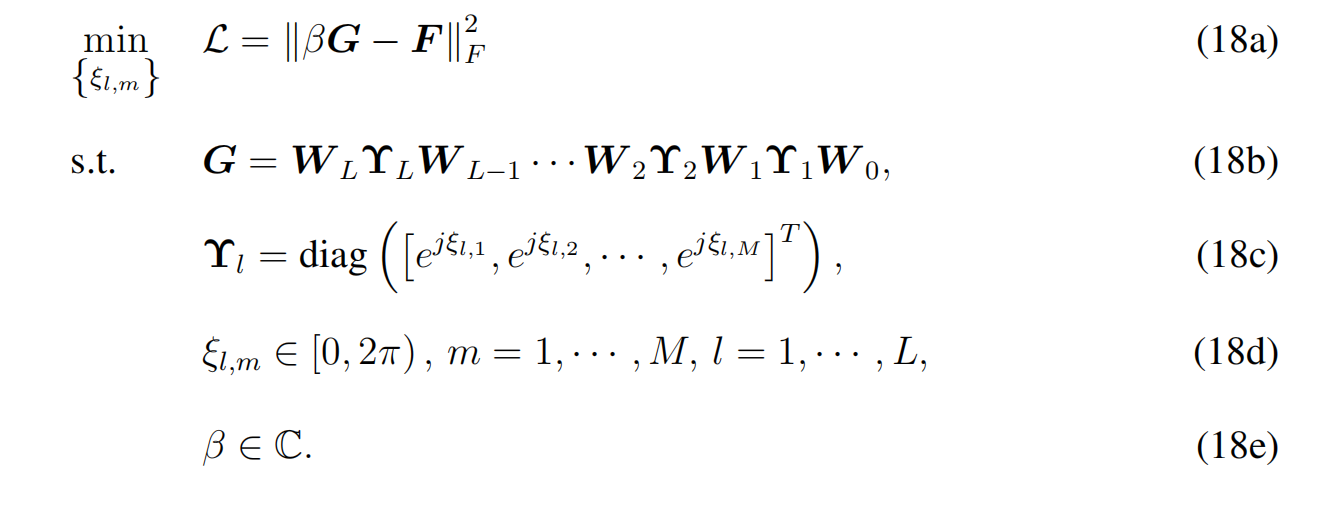
其中\(\mathbf{F}\)是2D DFT matrix,目的是将\(\mathbf{G}\)搞成和\(\mathbf{F}\)相同功能的东西,然后通过传播过程中自动计算
(空中计算)。
设计梯度下降算法进行求解。
Accuracy Improvement
没读懂
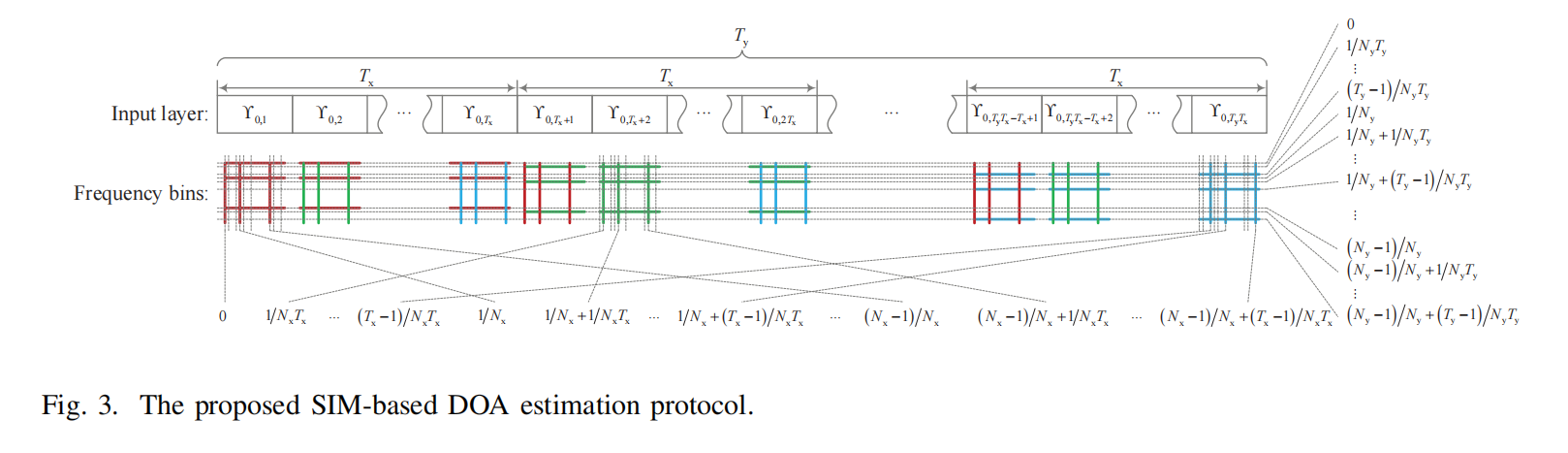


SIM实现了一个维度很小的DFT,这样只能返回一个很粗糙的on-grid 的离散估计值。通过在不同时刻调第 0 层的相移,这样可以生成一个不同频率格子DFT,每个时刻的频率格子是”正交“的,这样,可以通过增加快拍数,返回一个更精细的on-grid 估计值,
比如只关注一个俯仰角维度,2-point DFT,它划的格子对应的空间频率是0度,90度,比较空间谱能量,只能把来波方向(比如35度)测到0或者90这两个中的一个,但是可以通过调0层相移,把格子的频率给改了,改成1,91,再下一个时刻2,92,这样靠时间堆出来一个分辨率更高的格子,最后就能测出是35度。
Reference
- C. Liu, Q. Ma, Z. J. Luo, Q. R. Hong, Q. Xiao, H. C. Zhang, L. Miao, W. M. Yu, Q. Cheng, L. Li et al., “A programmable diffractive deep neural network based on a digital-coding metasurface array,” Nature Electronics, vol. 5, no. 2, pp. 113–122, Feb. 2022. ↩︎