STAR-RISs--Simultaneous Transmitting and Reflecting Reconfigurable Intelligent Surfaces
Date: 2024.03.18 10:50 Author: Joffrey LC
STAR-RISs: Simultaneous Transmitting and Reflecting Reconfigurable Intelligent Surfaces. Jiaqi Xu et.al. IEEE Communications Letters, September 2021 (pdf) (Citations 171)
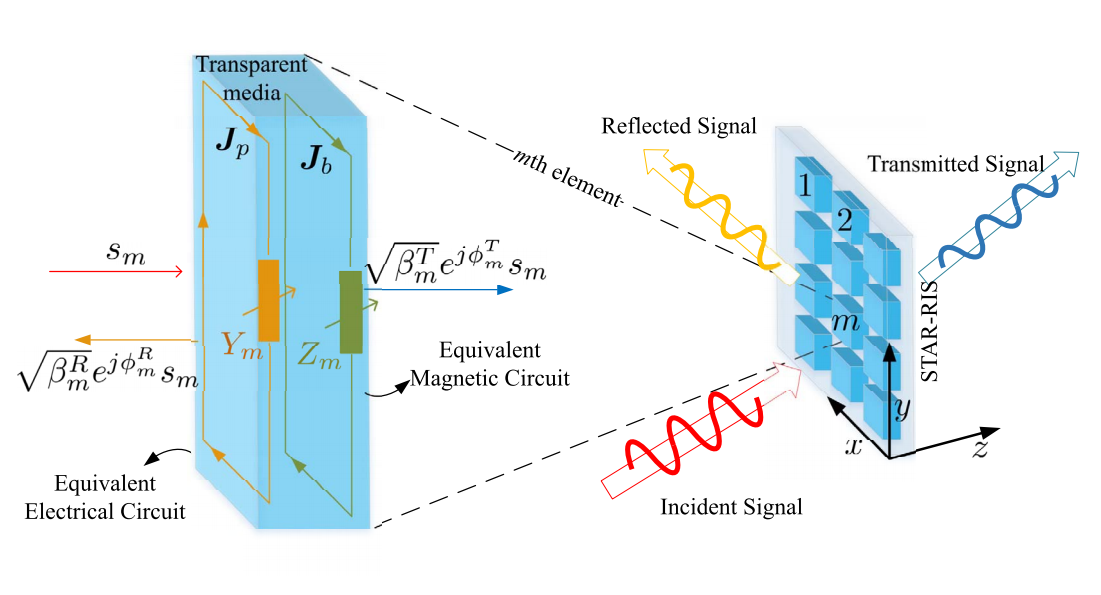
Quick Overview
Full diversity order can be achieved on both sides.
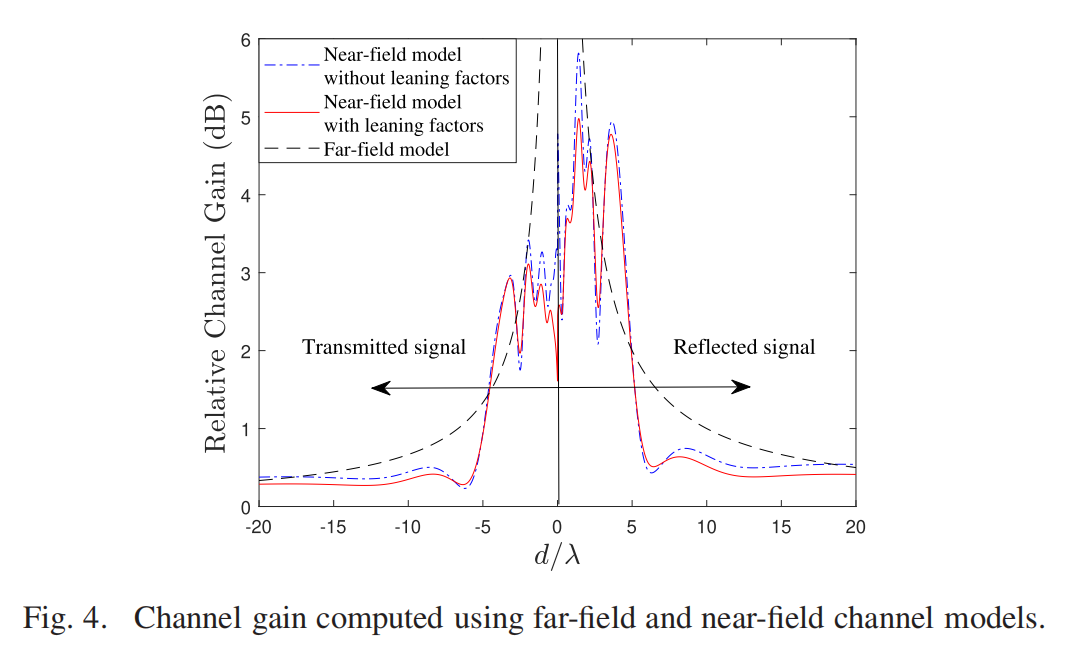
Far field and near field model
==The boundary between the near-field and the far-field is \(2L_a^2/\lambda\)，where\(L_a\) is the largest dimension of the RIS aperture.==
Far field
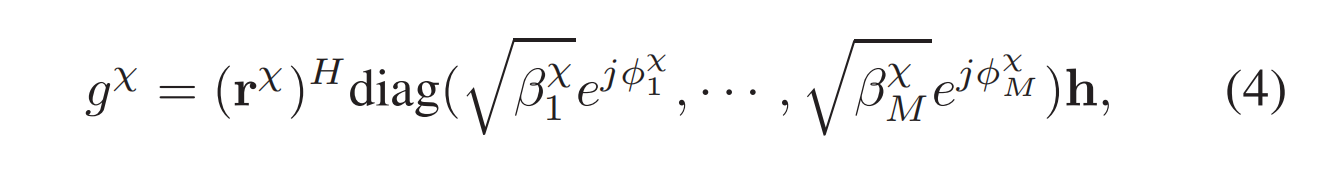
- 反射和透射的RIS相移可 independently adjusted
- 反射和透射有个功率分配，因为是passive，所以应该满足能量守恒
Near field
根据Fresnel-Kirchhoff diffraction formula，应该建模为\(M\)个单元的求和： \[
g^\chi=\frac{1}{j \lambda} \iint_{(\Sigma)} U^\chi(Q) F\left(\theta^\chi\right) \frac{e^{2 j \pi d_m^\chi / \lambda}}{d^\chi} d \Sigma
\] 
\[
g^\chi=\frac{A_e}{j \lambda} \sum_m \Phi_m^\chi h_m F\left(\theta_m^\chi\right) \frac{e^{2 j \pi d_m^\chi / \lambda}}{d_m^\chi}
\] 
\[
\left|g^\chi\right|=\frac{A_e}{\lambda}\left|\sum_m \Phi_m^\chi h_m\left(1+\cos \theta_m^\chi\right) \frac{e^{2 j \pi d_m^\chi / \lambda}}{2 d_m^\chi}\right| .
\] 
Diversity Analysis
All elements of STAR-RIS share the same power ratio, i.e., \(\beta^T_m=\beta^T,\beta^R_m=\beta^R,\forall m\in M\).
In fact, we can include the power ratios constrains of each element for further improving the performance.
定义diversity order：
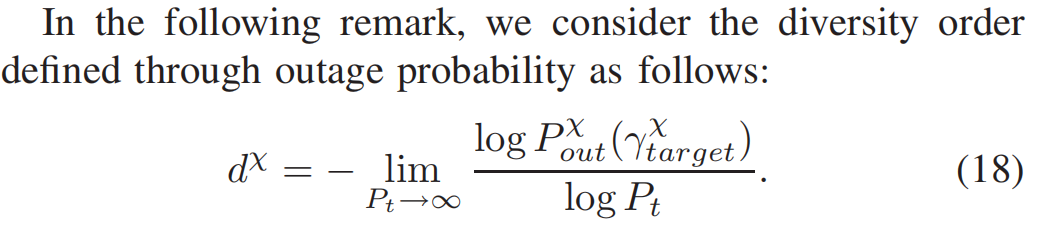
红色是考虑leaning factor/rate，而蓝色是没有使用leaning rate\(F(\theta)=1\)的
