知识储备-三角波/矩形波和梯形波频谱

工程上，很难实现完美的矩形波，所以讨论一下矩形波和三角波/梯形波的脉冲的频谱。

矩形波和三角波

时域波形

频域波形

从时域加窗的角度看待这个问题

可以观察到，二者的频谱的零点是一样的。但是，三角波明显衰减更快。这个点很有意思，在OFDM工程实现中，经常在时域加窗。

这个点不太好理解，因为一般从脉冲整形的角度出发，是在频域加窗，即时域卷积升余弦滤波器。但是这里是在时域上称升余弦，降低首尾的功率强度，等于在频域卷积sinc。

合理的解释是：

参考 CSDN

同样的，三角脉冲可以认为是加了窗的矩形脉冲，所以，其旁瓣被有效抑制。

矩形波和梯形波

看起来，只要保证整个：

梯形：上升沿+下降沿+稳定状态 = 矩形：稳定状态-上升沿

那么频谱的零点没有变化。

所以说，如果是占空比相同的形式，非完美的矩形波会导致零点偏移：

也许加成型滤波也是为了将这个零点压下去？

Test Code

clc;clear;close all;
% 参数设置
Fs = 10;            % 采样频率
T = 1/Fs;             % 采样间隔
t = -2:T:5;           % 时间向量（-2到5秒）
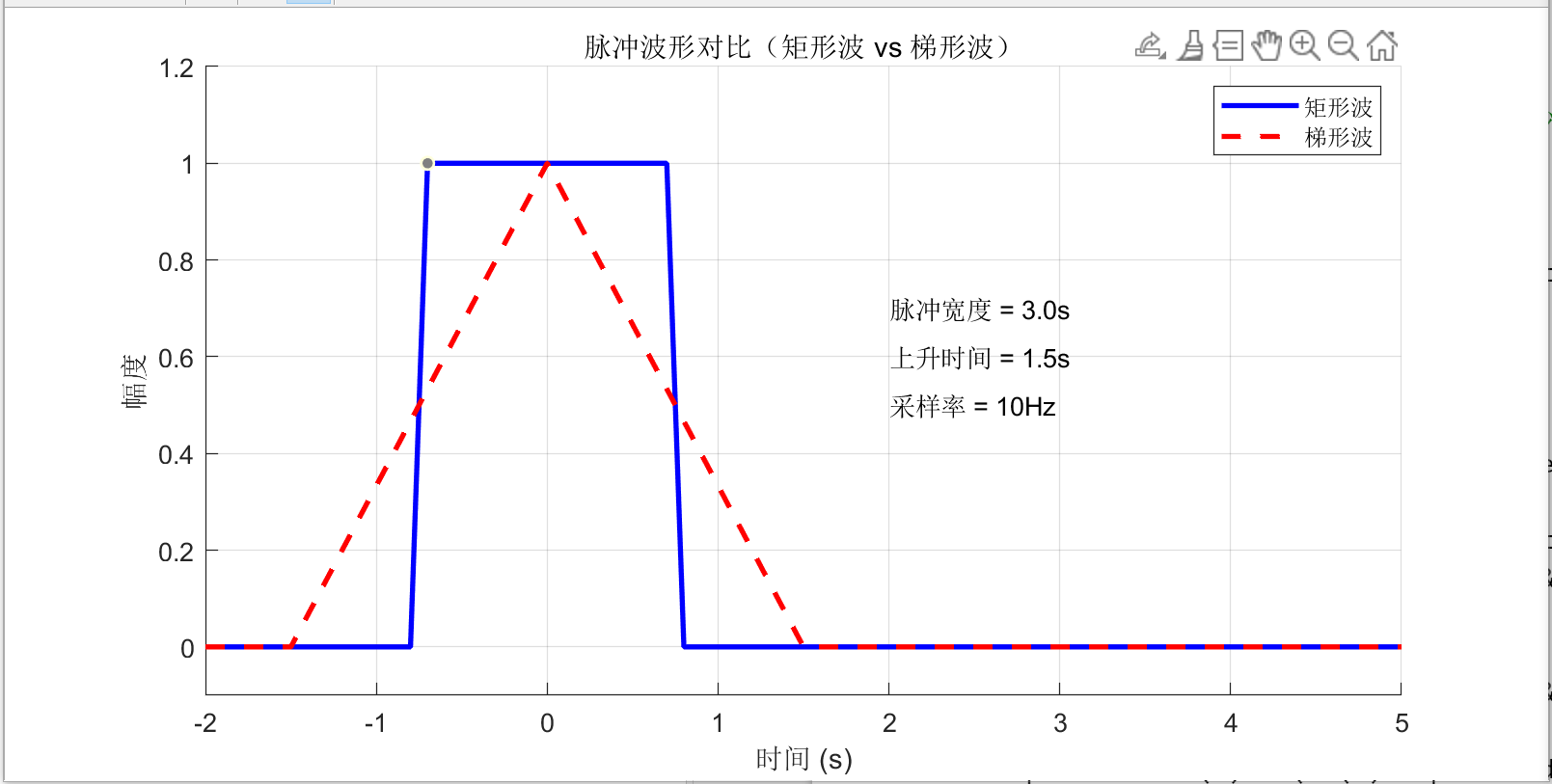
pulseWidth = 3;       % 脉冲总宽度（秒）
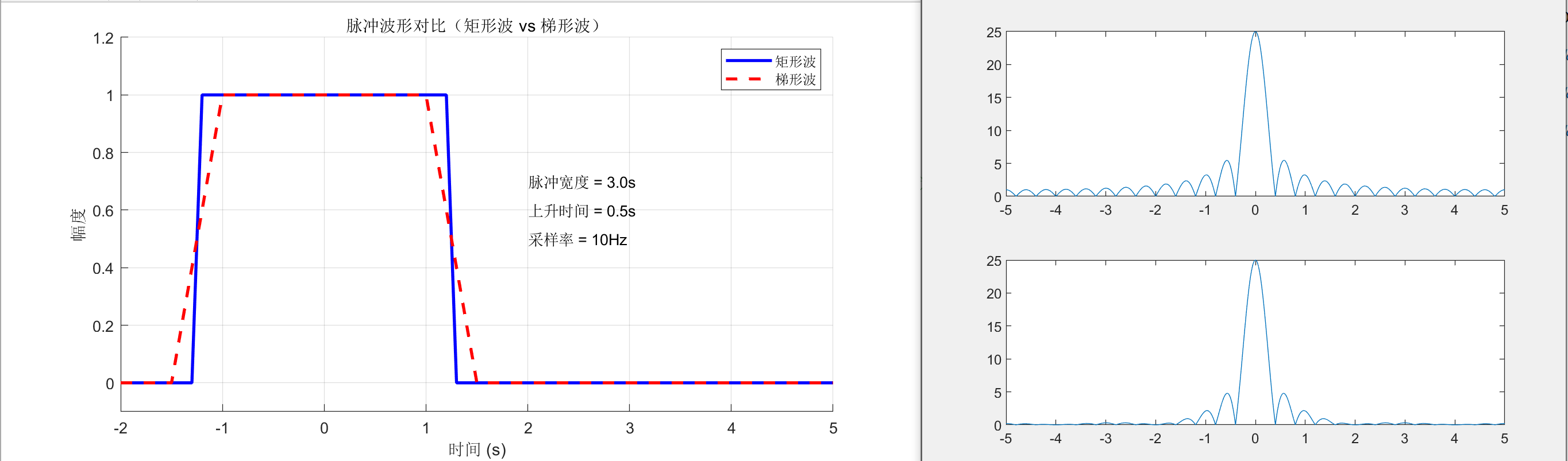
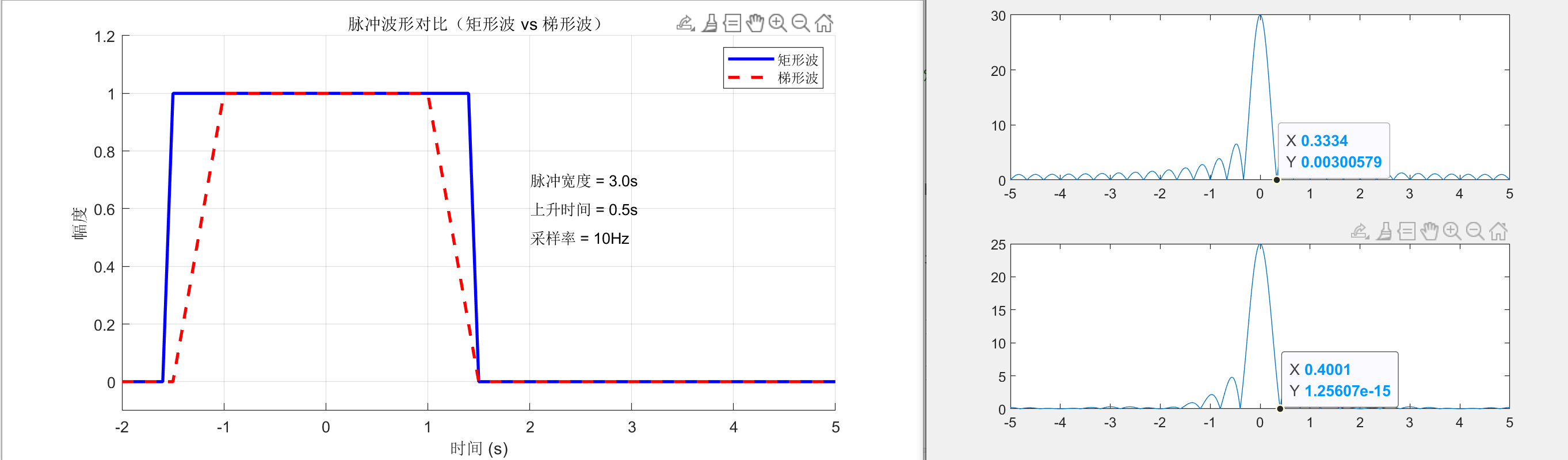
riseTime = 0.5;       % 梯形波上升/下降时间（秒）
amplitude = 1;        % 脉冲幅度

% 生成矩形波脉冲
rectPulse = amplitude * rectpuls(t, pulseWidth); % 生成以0为中心的矩形脉冲

% 生成梯形波脉冲
trapezoidPulse = zeros(1, length(t));
for i = 1:length(t)
    if t(i) >= -pulseWidth/2 && t(i) < -pulseWidth/2 + riseTime
        % 上升沿
        trapezoidPulse(i) = (t(i) + pulseWidth/2) / riseTime;
    elseif t(i) >= -pulseWidth/2 + riseTime && t(i) < pulseWidth/2 - riseTime
        % 平顶部分
        trapezoidPulse(i) = amplitude;
    elseif t(i) >= pulseWidth/2 - riseTime && t(i) < pulseWidth/2
        % 下降沿
        trapezoidPulse(i) = (-t(i) + pulseWidth/2) / riseTime;
    else
        trapezoidPulse(i) = 0;
    end
end

% 绘制对比图
figure('Color', 'white', 'Position', [100, 100, 800, 400])
hold on

% 绘制矩形波
plot(t, rectPulse, 'b', 'LineWidth', 2, 'DisplayName', '矩形波')

% 绘制梯形波
plot(t, trapezoidPulse, 'r--', 'LineWidth', 2, 'DisplayName', '梯形波')

% 图形美化
grid on
title('脉冲波形对比（矩形波 vs 梯形波）')
xlabel('时间 (s)')
ylabel('幅度')
xlim([-2 5])
ylim([-0.1 1.2])
legend('show', 'Location', 'northeast')

% 添加参数标注
text(2, 0.7, sprintf('脉冲宽度 = %.1fs', pulseWidth), 'FontSize', 10)
text(2, 0.6, sprintf('上升时间 = %.1fs', riseTime), 'FontSize', 10)
text(2, 0.5, sprintf('采样率 = %dHz', Fs), 'FontSize', 10)

set(gca, 'FontSize', 10)

nfft = 100000;
figure(100)
subplot(211)
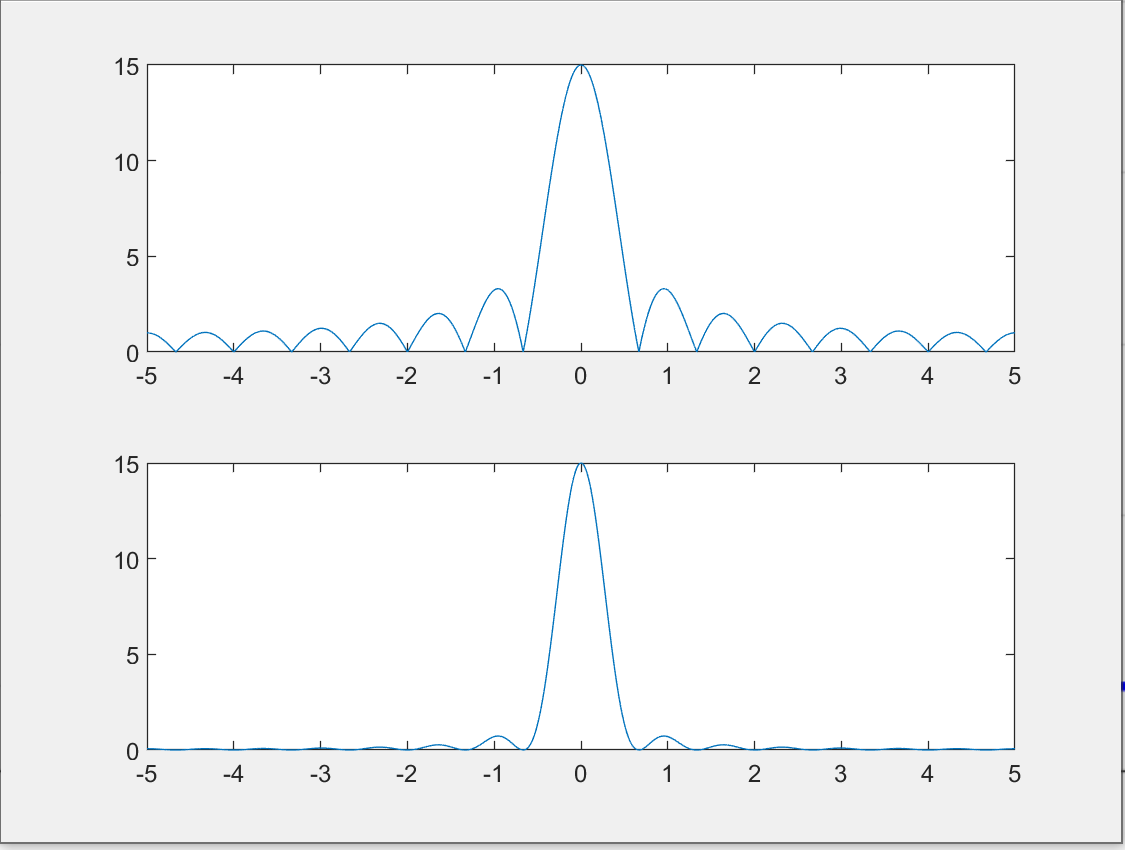
plot(((1:1:nfft)-ceil(nfft/2))/nfft*Fs, fftshift(abs(fft(rectPulse, nfft))))
subplot(212)
plot(((1:nfft)-ceil(nfft/2))/nfft*Fs, fftshift(abs(fft(trapezoidPulse, nfft))))